Mathematical modelling is the process of using mathematics to better understand real-world situations. Some mathematical models are incredibly complex, such as those used to predict the weather, the effect of increased carbon dioxide in the atmosphere, or the effect of a cut in taxation on small business activity. Others are simple, such as the instructions on medicine to calculate doses for children, or the cooking time for a roast.
In mathematical modelling, a formula or another well-defined method is developed to provide useful answers to practical problems. A good model is judged on the fit of the mathematics for the situation, rather than the complexity or ingenuity of the mathematical techniques used. Good mathematical models can be used again and again for different scenarios rather than just solving one specific problem.
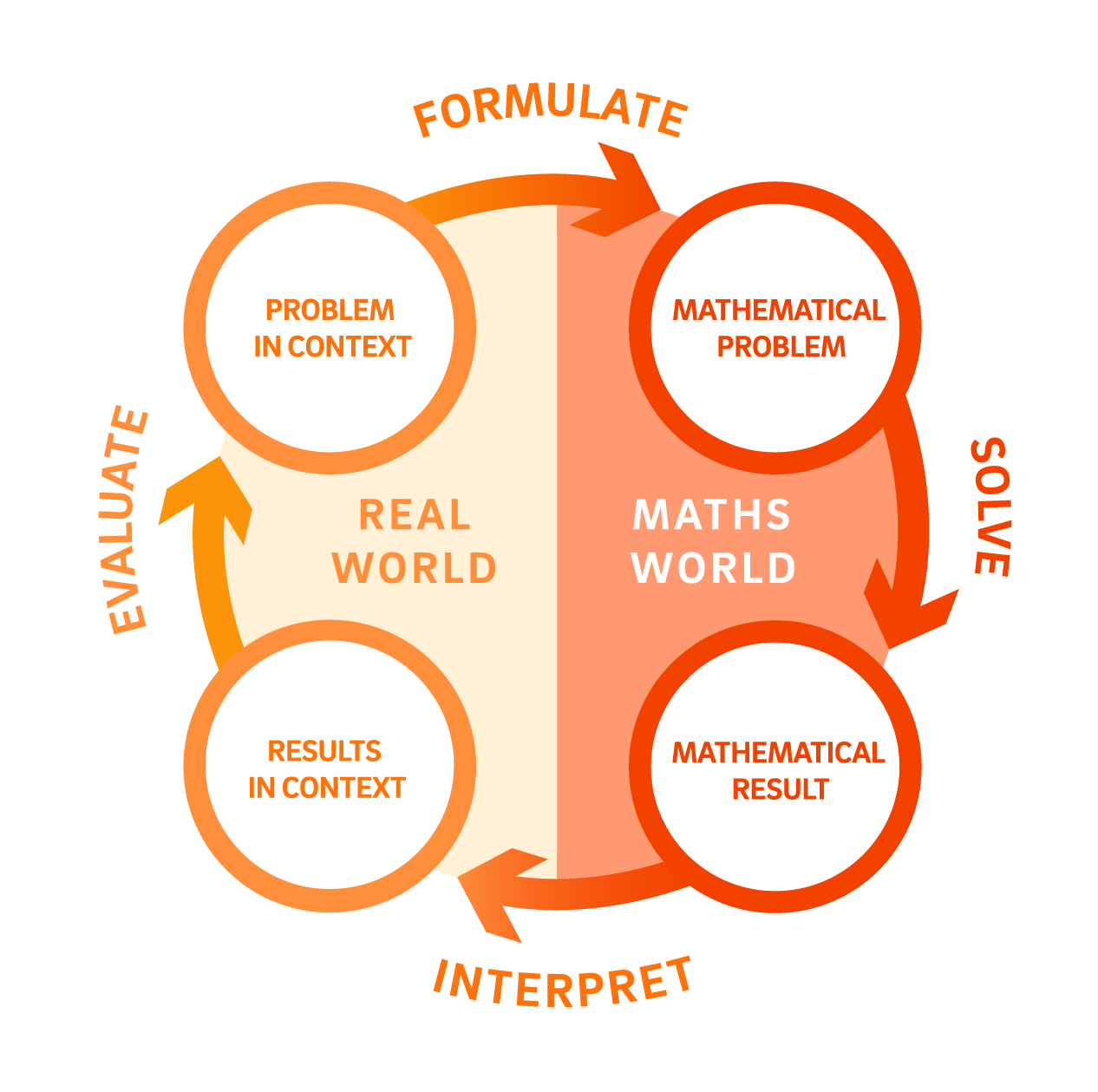
Mathematical modelling requires us to think about situations in two distinct ways. First, we make sense of the situation using our prior knowledge and lived experience. Next, we analyse and make sense of the situation mathematically.
- Modelling begins with real-world thinking by framing a problem in context. The first step is to understand the context and the problem well.
- A mathematical problem is formulated from this real problem, shifting thinking from the real world to the mathematical world.
- Within the mathematical world, mathematical activity solves the mathematical problem to produce a mathematical result.
- The mathematical result is then interpreted, determining what the result means in practice (results in context). This brings the process back from the mathematical world into the real world.
- Finally, the model needs evaluation: judging whether the solution provides an adequate and sensible answer to the real-world context. If yes, the model can now be used. If no, a new model can be formulated, beginning by thinking more about the real situation, and perhaps making different assumptions, including previously overlooked variables or by re-thinking the relationships between the variables.