Multiplicative relationships exist between numbers

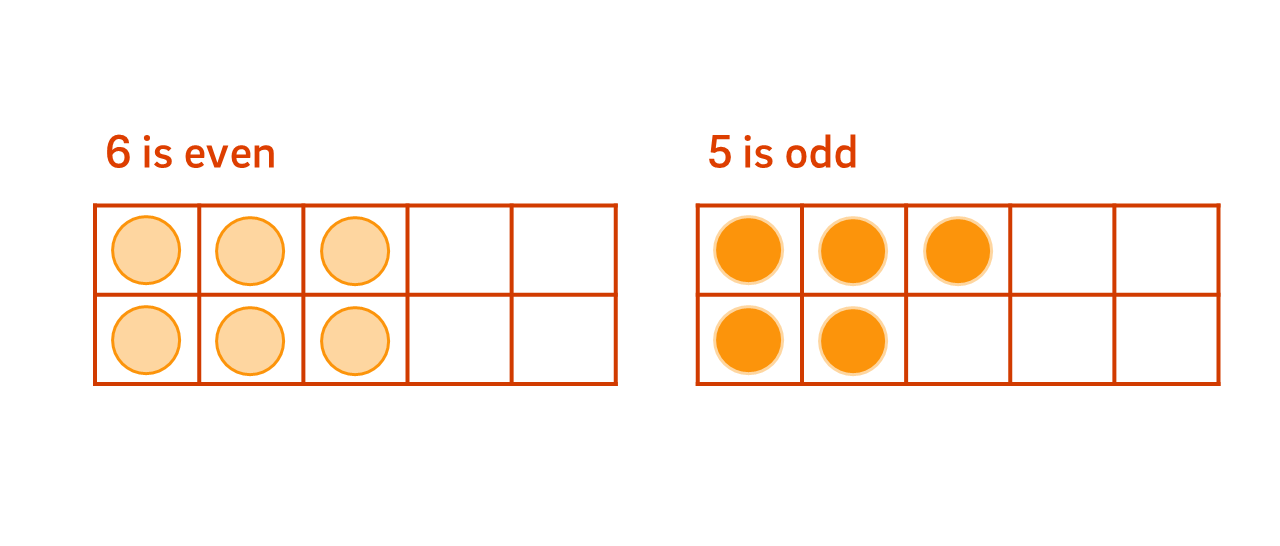
Each number has properties that make it unique. Some of these properties have multiplicative structures. For example, ‘oddness’ and ‘evenness’ are based on a multiplicative structure: An even number is divisible by two with no remainder. An odd number leaves a remainder of 1 when divided by two.

The multiplicative structures of these properties also create relationships between different numbers. These relationships reveal patterns in our number system and support efficient strategies for calculation and problem-solving.

Factors and multiples: Factors are numbers that divide exactly into another number without leaving a remainder. For example, 1, 2, 3, 4, 6, and 12 are factors of 12 because they divide 12 evenly. Multiples are the products obtained when a number is multiplied by whole numbers. For example, 12, 24, 36, and 48 are multiples of 12 because they result from multiplying 12 by 1, 2, 3, and 4, respectively.

Prime and composite numbers: Prime numbers are whole numbers greater than 1 that have exactly two factors: 1 and themselves. For example, 7 is prime because its only factors are 1 and 7. Composite numbers are whole numbers greater than 1 that have more than two factors. For example, 12 is composite because it has multiple factors: 1, 2, 3, 4, 6, and 12.

Prime factors: Every number greater than 1 can be expressed as a product of prime numbers in exactly one way.

Foundation

In Foundation, students recognise that some objects can be left over when sharing a collection between a given number of people. For example, 6 objects can be shared equally between 2 people, but when 7 objects are shared between 2 people one object is left over.

Year 1

In Year 1, students encounter a relationship between the number they are counting by and the position of the numbers they say when skip counting. For example, when we count by 2s we say every second number. Students also identify patterns in counting sequences. For example, when we count by 5s starting from zero all of the numbers end in 5 or 0. Skip counting is the foundation for creating and recognising sequences of multiples.

Year 2

In Year 2, students learn to recall and demonstrate proficiency with multiplication facts for 2s, and extend and apply these facts to establish related division facts. They recognise the relationship between doubling and halving: if double 7 is 14, then half of 14 is 7. Students continue to relate numbers in skip counting patterns to their position in the sequence when solving problems. For example, when calculating how many windows will be in 1, 2, 3, 4 … train carriages, students identify a relationship between the number of windows, the number of carriages and the number in the skip counting pattern. Students encounter equivalent multiplication facts as they represent different arrays for the same number. For example, they recognise that 6 twos are equal to 3 fours when rearranging an array for 12. Rearranging arrays provides the foundation for identifying factors.

Year 3

In Year 3, students learn to recall and demonstrate proficiency with multiplication facts for 3, 4, 5 and 10, and extend and apply these facts to develop the related division facts. They use part-part-whole and comparative models to represent multiplicative relationships between numbers when solving problems, and use their knowledge of relationships between and within numbers to select calculations strategies. A bar model can be used to represent multiplicative comparison problems. For example, Jay jumped 3 times further than Riley. If Riley jumped 2m how far did Jay jump?

The model clearly shows that Jay jumped 3 times 2m, to jump a total of 6m.

Students start to consider the properties of numbers to determine calculation strategies, such as using repeated doubling and halving or partitioning numbers into smaller parts to aid calculation. Students predict which numbers will or will not be effective for sharing a given quantity into equal groups without leaving a remainder and give reasons why, laying a further foundation for identifying factors.

Year 4

In Year 4, students learn to recall and demonstrate proficiency with multiplication facts to $10 \times 10$ and related division facts. They identify relationships between the multiplication facts for a number such as 3 and the multiplication facts for 6. They extend and apply multiplication facts to $10 \times 10$ to develop efficient mental strategies for computation with multiples of 10, 100 and 1000. They recognise that they can use a known fact such as $7 \times 4$ to calculate $7 \times 40$ as $7 \times 4 \times 10$, $7 \times 400$ as $7 \times 4 \times 100$, or $7 \times 4000$ as $7 \times 4 \times 1000$. Students explain and use the properties of odd and even numbers. They identify even numbers and explain why even numbers end in 2, 4, 6, 8 or 0 and why odd numbers cannot be divided by 2 without leaving a remainder. They generalise the results of multiplying by odd and even numbers: multiplying any number by and even number results in an even number; multiplying an odd number by an odd number results in an odd number.

Year 5

In Year 5, students use arrays, multiplication tables and materials to develop families of related multiplication and division facts. They express natural numbers as products of their factors, recognise multiples, and determine if one number is divisible by another. They identify all possible factors of a given number and use their knowledge to solve practical problems such as the possible dimensions of different rectangles with the same area. Students research divisibility tests and apply these tests to determine whether larger number are multiples of single-digit numbers. Students create algorithms that use multiplication and division facts to determine if a number is a multiple or factor of another number, identify lowest common multiples and highest common factors of pairs or triples of natural numbers, and use the fill down function of spreadsheets to generate sequences of multiples.

Year 6

In Year 6, students identify and describe the properties of prime, composite and square numbers and use these properties to solve problems and simplify calculations. They represent composite numbers as a product of their factors, including prime factors, and use this process to simplify calculations. Students apply the idea that the value of a digit becomes 10 times smaller each time the digit is moved a place to the right, a principle applied when multiplying and dividing by powers of 10. Exploring this idea reveals number patterns and relationships that emerge through multiplication and division.

Year 7

In Year 7, students describe the relationship between perfect square numbers and square roots and use squares of numbers and square roots of perfect square numbers to solve problems. For example, they use the relationship between perfect square numbers and their square roots to find the perimeter of a floor with an area of 81m².

Students represent natural numbers as products of powers of prime numbers using exponent notation.

Year 8

In Year 8, students apply algebraic properties to rearrange, expand and factorise linear expressions. They recognise the connections between expanded notation and exponent laws of products to apply exponent laws to calculate positive integer exponents. For example, they understand that $3^4 \times 3^3$ can be expressed as $(3 \times 3 \times 3 \times 3) \times (3 \times 3 \times 3) = 3^7$.