Equal groups and shares

Quantities can be arranged into equal groups or shares, with each group containing the same number of objects. Multiplication is the process of combining these groups, and division is the process of sharing the groups equally or forming equal sets. When quantities do not divide evenly, remainders are left over and can be interpreted in different ways depending on the context.

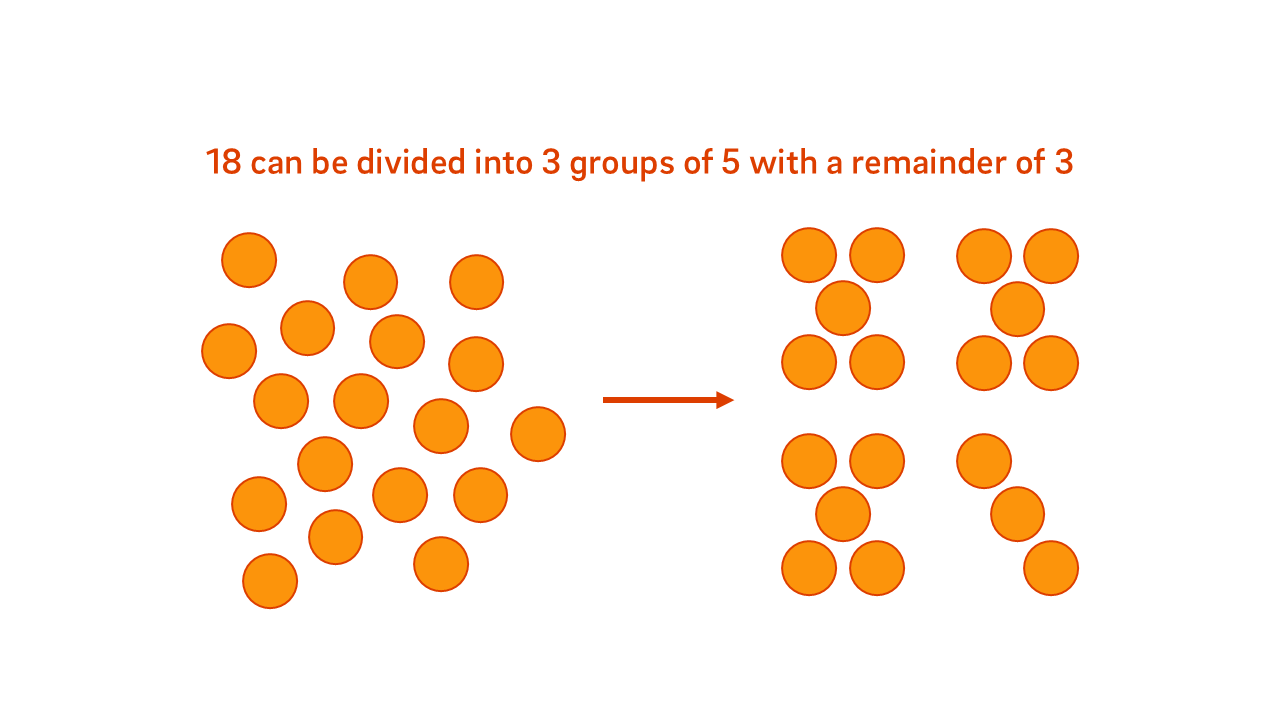
Arrays are a powerful visual model, illustrating the relationship between the number of groups (rows), the number in each group (columns), and the total quantity. Constructing and deconstructing arrays makes explicit the structure of multiplication and division and their inverse relationship.

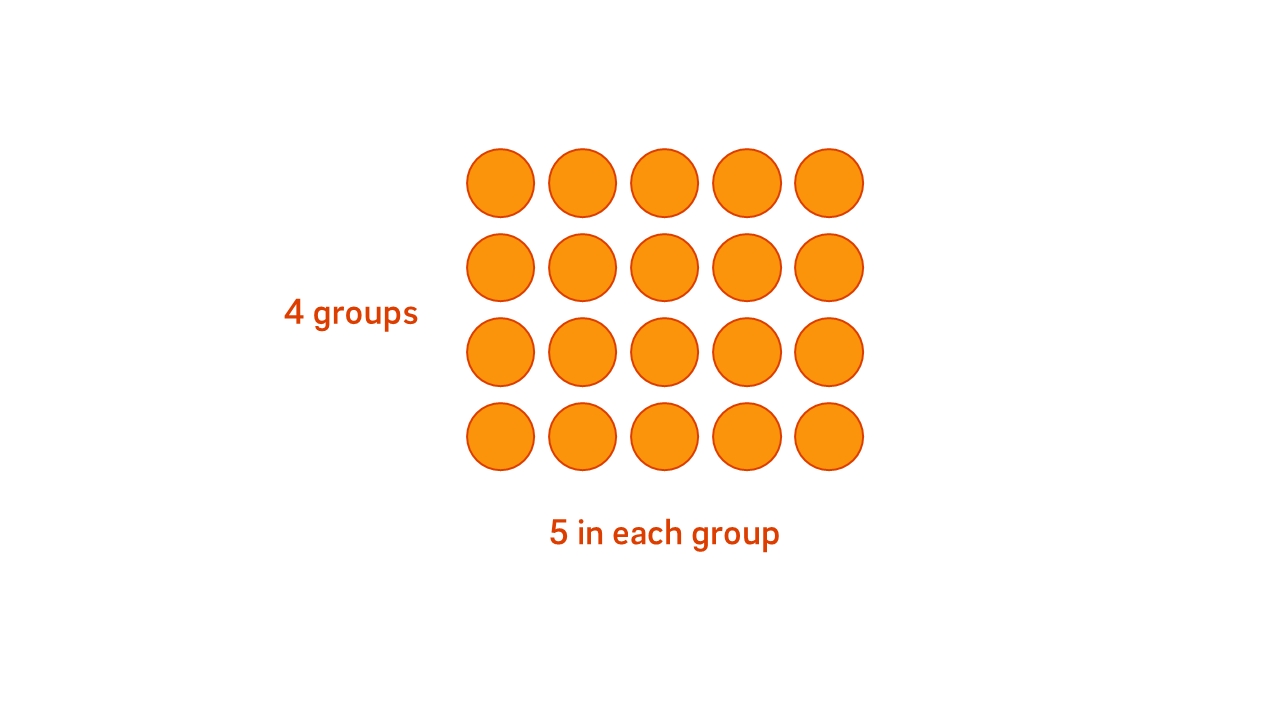
Foundation

In Foundation, students represent practical situations to quantify and equally share collections into groups. They reason about small collections and assign number names as they count in meaningful contexts. At this stage, students need opportunities to share materials in a variety of hands-on situations involving two or three participants. Their sharing may not always be equal, nor use the entire collection. They can often judge which group is larger by sight, though not necessarily by how much. They come to understand that a single collection can be partitioned in many ways, and when the parts are equal, it represents a fair share.

Year 1

In Year 1, students arrange collections into equal groups and shares to model practical problems. They draw and label representations to show the results of grouping and sharing. Through real-life experiences, students come to understand that quantities can be shared in different ways, and that partitioning a whole into equal parts means dividing it into groups of the same size without changing the overall quantity.

Students require extensive concrete experience, not only in the physical act of partitioning collections, but also in recognising how many parts have been made and how many objects are in each part. They begin to notice that the more people a collection is shared between, the smaller each share becomes. For example, when 12 is shared between 2 students, each receives 6; between 3, each receives 4; between 4, each receives 3, and so on. This ability to share a quantity into equal parts forms a foundational understanding for developing multiplicative thinking.

Year 2

In Year 2, students use arrays to represent problems involving equal groups and equal shares. Representing equal groups as equal rows and columns introduces the array as a powerful model that makes visible the relationship between the number of groups, the number in each group, and the total quantity. Students recognise that each row or column contains the same number of objects, and they use this structure to establish skip-counting patterns and represent repeated addition.

Students also come to understand the distinction between dividing a set into a given number of groups and dividing it into groups of a given size. Developing a deep understanding of equal sharing requires concrete experiences with both partitive division (dividing a whole into a given number of equal parts to find the amount in each part) and quotitive division (dividing a whole into equal parts of a given size to find how many parts). For example, students might share 24 counters between 6 students to determine how many each student receives (partitive) or group the counters into sets of 6 to determine how many students receive a share (quotitive).

Through constructing and deconstructing arrays, students solve a range of grouping and sharing problems, and record their thinking using repeated addition and repeated subtraction as computational strategies.

Year 3

In Year 3, students learn to write multiplication and division number sentences to represent problems involving equal groups and shares.

Students create problem scenarios that can be represented using multiplication and division expressions. Arrays serve as a visual model for counting equal groups, where the number of rows (how many) changes while the number in each row (how much) remains constant. This is evident when students learn multiplication facts, such as: one group of three is three, two groups of three are six, three groups of three are nine, and so on. The emphasis is on the size of the group and the process of repeatedly adding or skip counting by this number (e.g. 3, 6, 9, 12...).

Students build on their understanding of arrays to represent multiplication as number sentences of the form:

how many × how much = the whole

The two-dimensional structure of an array supports students to distinguish between the number of rows (how many groups) and the number in each row (how much in each group), both of which contribute to the total quantity.

Students construct arrays to represent multiplication and deconstruct them to solve division problems. For example, to divide using an array, they can create equal rows of a known size and determine how many rows are formed. The inverse relationship between multiplication and division becomes visible as students use known multiplication facts to solve division problems.

In multiplication, students typically know the number of groups and the size of each group but need to find the total (the whole). In division, they know the whole and either the number of groups or the group size, and must determine the unknown quantity. As students work flexibly with arrays, they begin to see how the array model connects the whole, the number of groups (how many), and the group size (how much), allowing them to solve for the unknown in a variety of contexts.

They also begin to apply their understanding of the multiplicative structure to identify totals in partially covered arrays, using number facts and visual reasoning to determine missing quantities.

Year 4

In Year 4, students represent practical grouping and sharing problems using diagrams and arrays to clarify what is known and what is unknown. They write multiplication and division number sentences and select efficient mental and written strategies to solve these problems.

The array remains a valuable model and can be used in two ways:

• as a discrete model, representing equal groups with blocks or counters arranged in rows and columns.
• as a continuous area model, using a rectangular grid to represent multiplication and division within a spatial context.

Both representations support students in developing and recording multiplication and related division facts up to 10 × 10.

Students increasingly recognise connections between known multiplication and division facts to derive new facts. The inverse relationship between multiplication and division becomes more explicit as students draw on known multiplication facts to support division reasoning.

Clarifying what is known and what is not helps students choose effective strategies and apply inverse reasoning. For example, when solving 72 ÷ 6, students may find it easier to ask “What times 6 equals 72?”—reframing the division problem using a known multiplication fact. In this case, the whole (72) and the group size (6) are known, and the unknown is how many groups of 6 can be made.

Year 5

In Year 5, students extend their understanding to multiply larger numbers by one- or two-digit multipliers to solve problems involving equal groups. They use their knowledge of equivalent number sentences to solve for unknown values in multiplication and division problems that involve operations on both sides of an equation. For example. 3 × 5 = 30 ÷ ?.

Students begin to formalise the structure of multiplication, moving from the intuitive “how many × how much = whole” to a more abstract understanding:

factor × factor = product

They learn to choose efficient calculation strategies, use digital tools appropriately, and check the reasonableness of their answers. Students use the array to apply the distributive property of multiplication when multiplying large numbers by decomposing them into parts. This relies on a strong understanding of place value, particularly regrouping and renaming (see The properties and principles of multiplication and division facilitate efficient calculation).

The array model helps ensure that each part of one factor is multiplied by every part of the other. For example, using area models or grid methods, students multiply multi-digit numbers by decomposing them and applying the distributive property. This same model can also be adapted to support division with larger numbers, reinforcing the connection between multiplication and division.

Year 6

In Year 6, students choose and evaluate efficient calculation strategies to solve grouping and sharing problems, including those involving decimals. They continue to use digital tools where appropriate and estimate to assess the reasonableness of their solutions.

Students extend their understanding of division by learning to interpret remainders as fractions or decimals. For example, when dividing 26 by 4, they recognise that the quotient includes 6 complete groups with a remainder of 2. This remainder can be expressed as a fraction (6 2/4 or 6 1/2) or as a decimal (6.5). They begin to see how decimal and fractional representations of remainders reflect the part-whole relationship of numbers, strengthening their number sense and flexibility with division.

Year 7

In Year 7, students extend their earlier work with arrays and area models to solve grouping and sharing problems involving fractions and decimals. They use visual models such as fraction walls, rectangular arrays, algebra tiles, and informal jottings to solve increasingly complex grouping and sharing problems involving fractional and decimal quantities.

Students need substantial experience working with the area model of arrays to represent and make sense of the multiplication and division of fractions. This experience deepens their understanding of part-whole relationships and supports their transition from arithmetic to algebraic thinking. Through this work, students build the conceptual foundations needed to generalise and apply multiplicative structures in more abstract contexts, including algebra.

Year 8

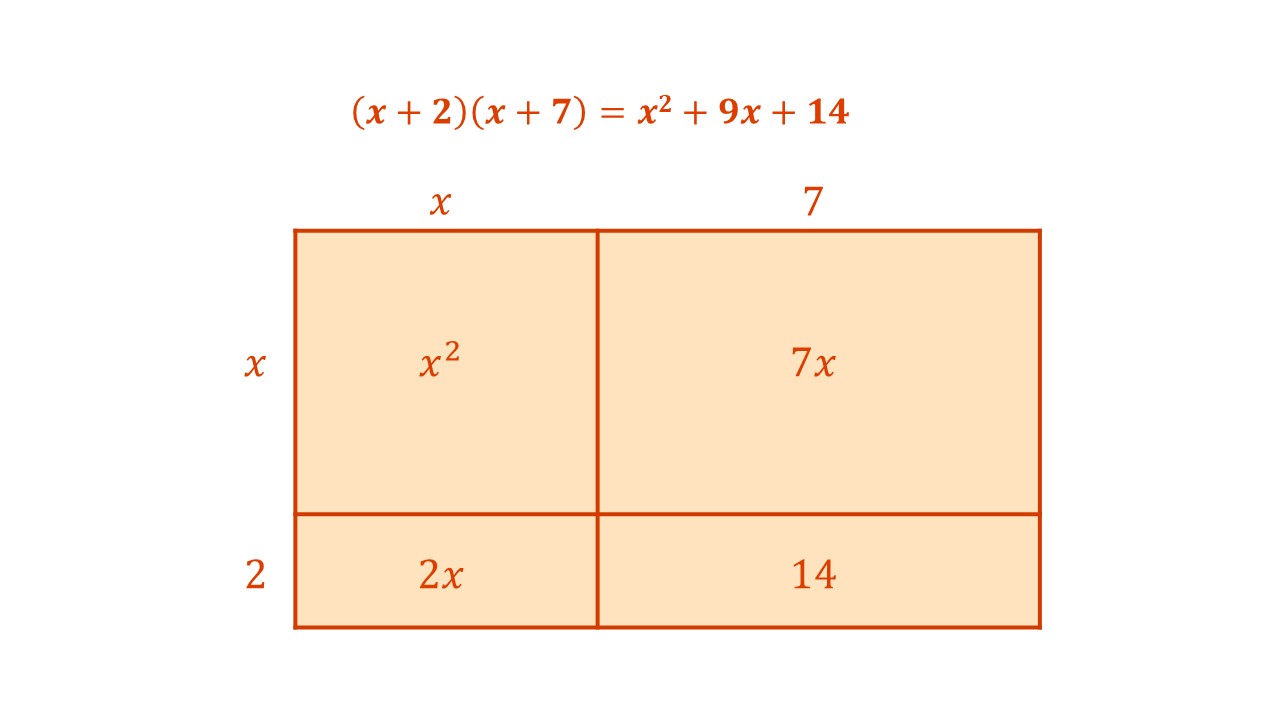
In Year 8, students extend their understanding of multiplicative structures into more abstract algebraic contexts. Building on earlier work with arrays and area models, they apply these visual representations to algebraic expressions, including the multiplication and expansion of binomials. The array and area models continue to support students’ understanding of the distributive property and provide a meaningful link between arithmetic and algebra. For example, students use area models to represent expressions such as $(x + 2)(x + 7)$, seeing how each term is multiplied and how the products contribute to the expanded form.