Many of these are 1 of those

Quantities can be partitioned into equal-sized parts that are understood as composite units rather than collections of individual items. This process, known as unitising, involves recognising that many of these are 1 of those, and enables reasoning with collections rather than counting individual objects.

The two-dimensional structure of arrays supports the transition from additive thinking—partitioning and recombining parts—to multiplicative reasoning about the relationships between parts and the whole. Arrays reveal the connections between the number of groups, the number in each group, and the total quantity, illustrating that multiplication combines factors to produce a product, with each factor representing a composite unit.

Many of these are 1 of those links to the powerful mathematical idea in place value that 10 of these is 1 of those. In this context, groups of ten are combined to form a single unit, highlighting the base-10 structure of our number system.

Foundation

In Foundation, students begin to recognise that a number of objects can form a group, and can identify how many objects are in each group through modelling practical situations. Students reason about small collections and start to assign number names as they count. At a glance, they can often see that a collection is made up of smaller groups of one, two, or three objects, and accurately name these quantities. This ability, known as subitising, is crucial for developing mental representations of numbers. Extensive experiences with subitising collections of up to ten items support students in seeing numbers as countable units, rather than counting by ones.

Developing the capacity to trust the count—to believe that numbers are consistent and reliable—is fundamental. It underpins the understanding that all numbers are composed of smaller parts. This part-part-whole knowledge is essential for developing the concept of a composite unit. For example, recognising that five can be made up of four and one, or three and two, shows that a collection can be partitioned in multiple ways without changing its total value. Students also learn that collections can be divided into equal parts in different ways, and when the parts are of equal size, this is understood as a fair share (see Quantities can be arranged in equal groups and shares).

Year 1

In Year 1, students begin to distinguish between the number of groups or shares and the quantity within each group or share. For example, when sharing 15 objects between 3 people, they learn to recognise that there are 3 shares and that each share contains 5 objects. They also model simple situations involving many-to-one correspondence. For instance, if one tricycle has 3 wheels, how many wheels do 4 tricycles have? Extending this to 8 tricycles introduces opportunities for students to move beyond a simple make-all, count-all strategy. They may begin to use strategies such as doubling or making connections between known problems (Siemon et al., 2011).

Students use one-to-one correspondence to share and count, distributing items equally by giving one, two, or three at a time to each person. They can then identify how many are in each share. However, at this stage, students may focus primarily on how many are in each group, rather than recognising that the number of groups can also be counted. To support this, they need extensive experiences working with numbers 2-10 as countable units before engaging in more complex, informal work with groups.

Year 2

In Year 2, students begin to describe arrays by identifying the number of rows or columns and the number of objects in each. They recognise that each row or column represents a set number of objects and start to contract the language they use from “1 row of five is 5” to “1 five is 5, 2 fives are 10…” and so on.

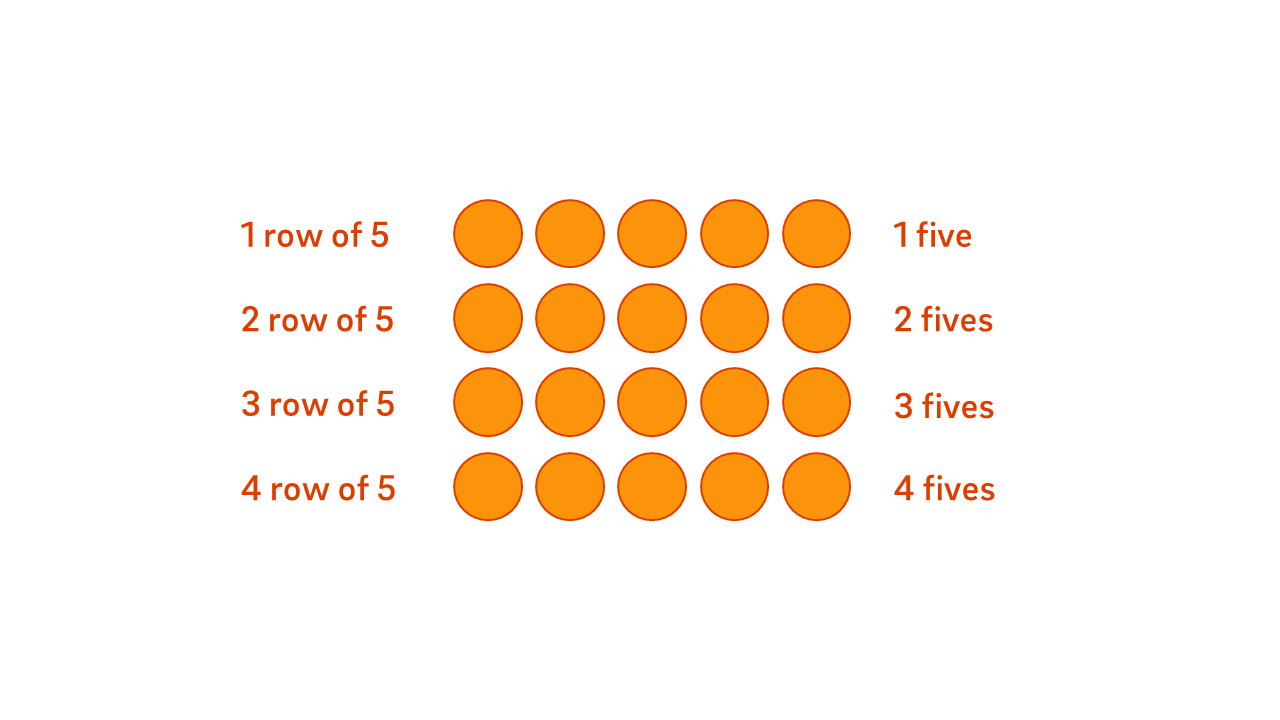
At this stage, students are learning to coordinate two aspects of counting: the number of groups and the size of each group. This marks a shift in thinking from counting all objects one by one to understanding collections of ones as composite units. For example, seeing a group of five ones as a single unit—a “five”—allows students to count in multiples: “1 five, 2 fives, 3 fives...”.

It is important to distinguish between two ways of thinking:

• How many: focusing on the total count (e.g. 5, 10, 15, 20).
• How much: focusing on the unit structure (e.g. 1 five, 2 fives, 3 fives, 4 fives).

Initially, students may not notice that the groups are equal in size and may perceive them as separate, unrelated sets. They need extensive experiences working with arrays to develop their capacity to simultaneously hold both the number of groups and the quantity in each group in mind. This understanding supports their progression from using additive thinking to find the whole amount to reasoning multiplicatively.

Year 3

In Year 3, students apply the idea that “many of these are 1 of those” and begin to represent this in multiple ways. Through experiences with partitioning and recombining parts, they develop a deeper understanding of multiplicative part-whole relationships. The two-dimensional structure of an array supports this thinking. For example, when students create an array of 24 by combining 4 rows of 6, they simultaneously see how the three elements—number of rows, number in each row, and the whole amount—interact. They understand that 4 rows of 6 make 24, and conversely, that 24 can be partitioned into 4 groups of 6, highlighting the inverse relationship between multiplication and division.

Rotating the array 90° to show 6 rows of 4 also demonstrates the commutative property of multiplication (see The properties and principles of multiplication and division facilitate efficient calculation for more detail). As students explore these relationships, they begin to connect multiplication and division facts and use known facts to derive related ones.

Students also begin to use the array as an “area” or “region” model, visualising a rectangular grid made up of intersecting rows and columns. They see that the product of the array is composed of composite units—its rows and its columns. Over time, their perception of the array shifts from a collection of discrete counters to a more abstract, continuous model made up of intersecting composite units.

Year 4

In Year 4, students solve practical problems involving money. They use their fluency with basic multiplication facts to estimate results efficiently. To do this, they need a flexible range of mental strategies and partitioning techniques. For example, to estimate the cost of 5 packets of biscuits at $2.60 each, a student might reason that $2 per packet would total $10, and $3 per packet would total $15—so the actual cost must fall between $10 and $15, and closer to $15.

Students also extend their understanding of multiplication to solve multiplicative comparison problems. For example, if Ben has saved $37.50 and this is five times the amount Amy has saved, students must reason about the relationship between these amounts. They know the total and the multiplicative comparison (five times as much) and must determine Amy’s savings. To solve and justify their reasoning, students are encouraged to model the situation and explore the connection between the quantities involved.

Year 5

In Year 5, students solve rate problems involving the division of larger numbers. Context is key, particularly when a division results in a remainder, as this affects how the solution is interpreted. For example, if students are calculating how many buses are needed to transport a group of passengers and each bus holds a fixed number of people, any remainder means an additional bus is required. In contrast, if the problem involves sharing money among people, the remainder may be expressed as a decimal fraction.

Year 6

In Year 6, students model rate situations involving earning money and budgeting to solve practical problems such as “Can I afford it?” and “How long will it take me to save for it?”. They model real world applications of percentages to interpret discounts and understand their impact on price.

A key concept is that 100% represents the whole, and students should encounter percentage problems in meaningful contexts. Through these, they learn to interpret and use models to describe, represent, and compare relative sizes. They also develop the ability to use these models to communicate and justify their thinking.

Year 7

In Year 7, students learn to model practical situations involving proportional reasoning. They extend their understanding from “many of these are 1 of those” to more general relationships, such as “many of these relate to a different number of those”, as they begin to recognise, represent, and solve problems involving ratios.

Students use diagrams and concrete materials to represent ratios and develop an understanding that a ratio expresses the quantitative relationship between two or more groups. They apply this knowledge in real-world contexts, such as dividing quantities of a given ratio—for example, mixing 500 mL of liquid in a concentration of 1:4.

Ratios can be expressed in two key ways:

1. Multiplicative comparison: comparing two distinct quantities to determine how many times greater one is than the other. For example, if a jug contains 1 cup of juice and 4 cups of water, the ratio is 1:4. This is not a fraction, as it compares two separate quantities (juice and water).
2. Composed unit: combining two related quantities into a single unit. For example, if 4 lemons cost $1.00, the composed unit is 4 lemons per $1.00. This can also be interpreted as a unit rate: $1.00 ÷ 4 = $0.25 per lemon, or a ratio of 1:4 when considering dollars to lemons.

Year 8

In Year 8, students deepen their understanding of proportional reasoning by exploring relationships such as “many of these relate to a different number of those”. They use mathematical modelling to represent and solve problems involving ratios, percentages, and rates in practical contexts.

For example, students might explore how to form a group with a ratio of 2:1 adults to children and a ratio of 10:11 males to females, ensuring the group includes at least one adult, one child, one male, and one female. To do this, they must work with both ratios simultaneously, finding a total group size that satisfies both constraints. This involves defining variables and determining the lowest common multiple to preserve the composition of the group.

Through this process, students develop an understanding of covariation—recognising that when both quantities in a ratio are scaled by the same factor, the overall proportion remains constant. This helps them reason flexibly about ratio-based relationships in increasingly complex scenarios.