Multiplication: What is a Plocoroo?
View Sequence overview“For each” is a key multiplicative idea.
Tree diagrams make the multiplicative structure in “for each” problems visible by showing how each choice connects to several others.
Whole class
What is a Plocoroo? PowerPoint
A large copy of What is a Plocoroo?, created by printing What is a Plocoroo Pictures on A3 or A4 paper. Staple or bind as indicated and then cut each picture along the dotted lines.
Animal cards printed onto A4 or A3 paper
Each group
A small copy of What is a Plocoroo?, created by printing What is a Plocoroo Pictures on A4 or A5 paper. Staple or bind as indicated and then cut each picture along the dotted lines.
Task
Use the large copy of What is a Plocoroo? to introduce the book to the students.
Provide groups of students with a small copy of What is a Plocoroo? and invite them to explore the book by creating their own Plocoroo, as well as experimenting with other animal combinations.
Explain that the book has been made using ten different animals, with each animal cut into three parts: a head, a body, and a tail.
Pose the question: How many different animals can be made using this book?
Finding maths in the everyday

Mathematics is all around us—we can even find it on our bookshelves! A flip book provides a playful and imaginative way for students to explore mathematical ideas. As they flip through different animal heads, bodies, and tails to create new creatures, they are engaging with an important mathematical concept: Cartesian product. Each unique creature represents one possible combination, showing how multiple sets of options can be combined to form new possibilities.
Through this context, students investigate the multiplicative structure that underpins “for each” problems. They come to see that for each head, there are several possible bodies, and for each of these head-body combinations, there are several possible tails. By representing these relationships in a tree diagram, students will make the multiplicative structure visible and recognise how the total number of combinations can be found by multiplying the number of options for each part.
Mathematics is all around us—we can even find it on our bookshelves! A flip book provides a playful and imaginative way for students to explore mathematical ideas. As they flip through different animal heads, bodies, and tails to create new creatures, they are engaging with an important mathematical concept: Cartesian product. Each unique creature represents one possible combination, showing how multiple sets of options can be combined to form new possibilities.
Through this context, students investigate the multiplicative structure that underpins “for each” problems. They come to see that for each head, there are several possible bodies, and for each of these head-body combinations, there are several possible tails. By representing these relationships in a tree diagram, students will make the multiplicative structure visible and recognise how the total number of combinations can be found by multiplying the number of options for each part.
Allow students time to explore the problem in their groups. Ask students to represent their thinking in ways that are meaningful to them.
After students have had time to experiment, highlight the challenge of working with all ten animals. Explain that mathematicians often begin with a simpler version of a problem and then use what they learn to tackle more complex ones.
Encourage the students to think about how a simpler problem might be used to help solve the problem. For example, two different ways this problem can be simplified include:
- What if there was just one head? How many combinations can be made with one head, ten bodies and ten tails?
- What if there was just one animal? What if there were just two animals? What if there were three?
What if there was just one head?
- Starting with just the shark head, there are ten bodies. For each body there are ten tails.
- Using this, we can generalise for ten heads. For each head in the book there are ten possible bodies: 10 heads × 10 bodies. For each of these bodies there are ten tails: 10 heads × 10 bodies × 10 tails.
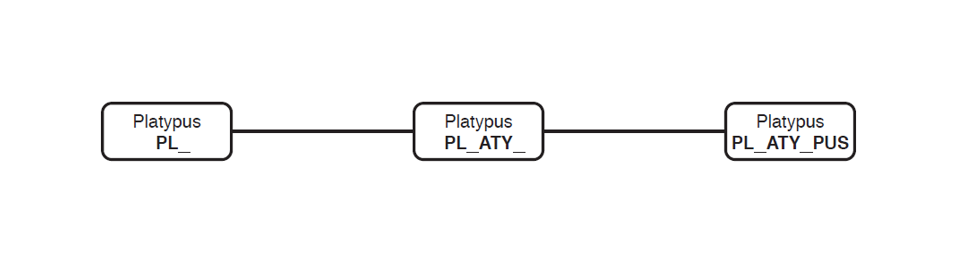
What if there is just one animal?
- For each head there is only one body: 1 head × 1 body.
- For each body there is only one tail: 1 head × 1 body × 1 tail. This gives one animal.
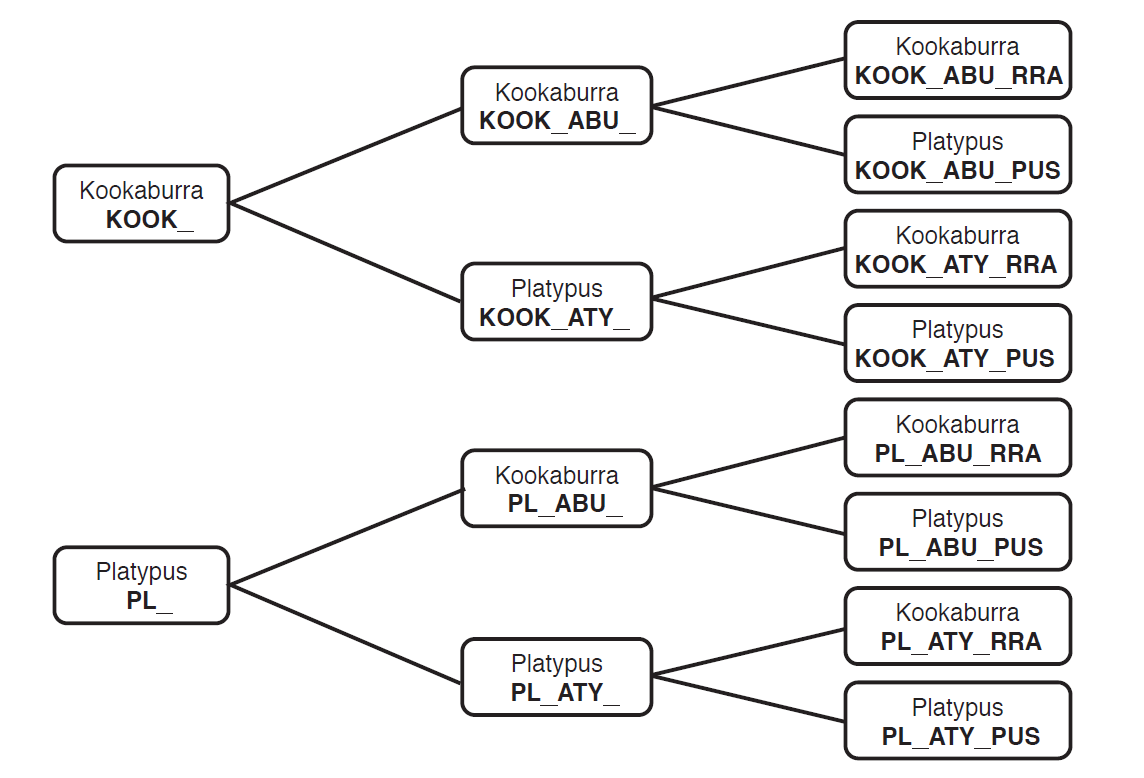
What if there are two animals?
- For each head there are two bodies: 2 heads × 2 bodies.
- For each of these bodies there are two tails: 2 heads × 2 bodies × 2 tails. This gives eight different animals.
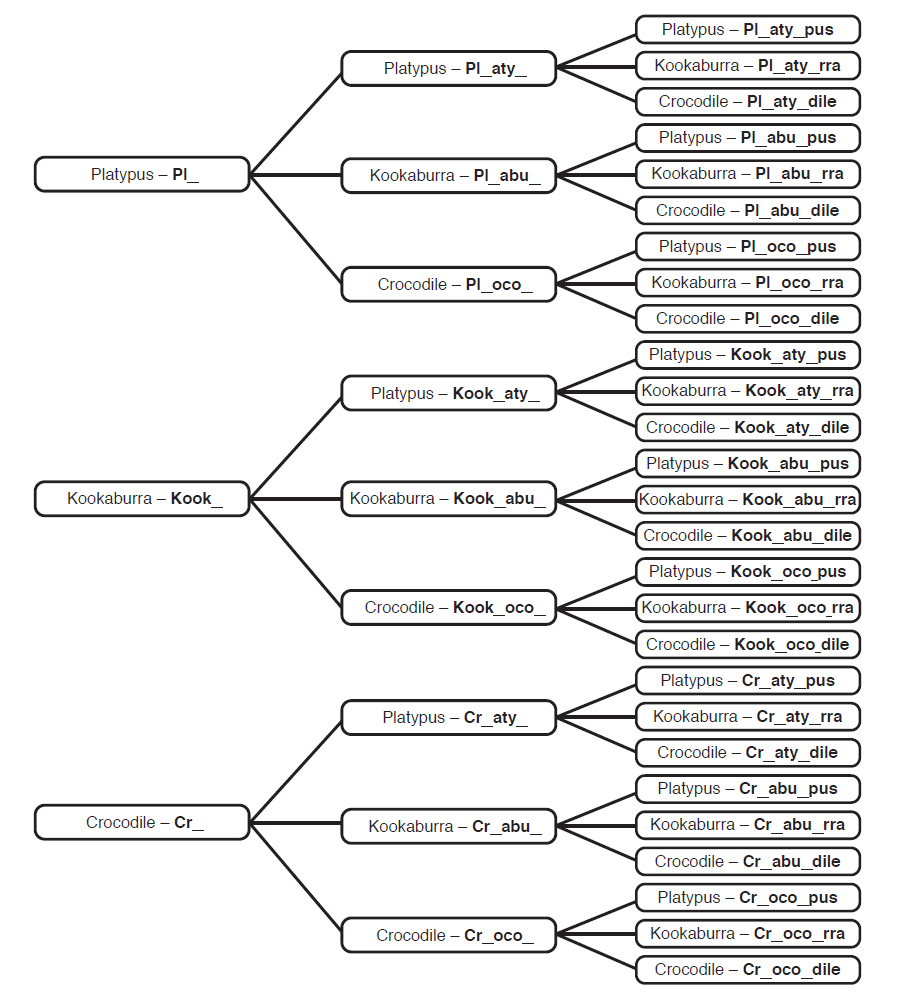
What if there are three animals?
- For each head there are three bodies: 3 heads × 3 bodies.
- For each of these bodies there are three tails: 3 heads × 3 bodies × 3 tails. This gives 27 different animals.
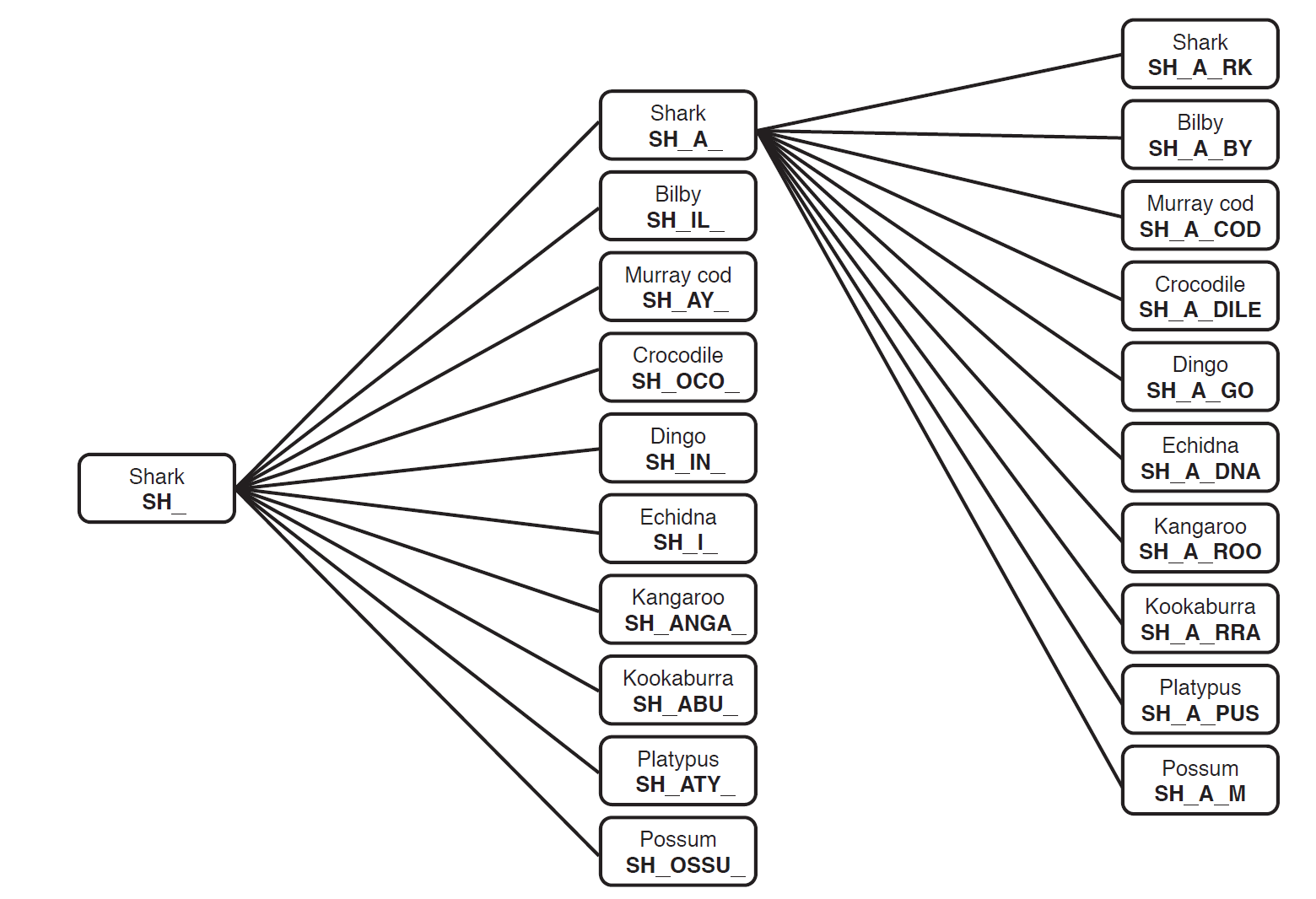
What if there are ten animals?
- For each head there are ten bodies: 10 heads × 10 bodies.
- For each of these bodies there are ten tails: 10 heads × 10 bodies × 10 tails. This gives 1000 different animals.
Multiplication as “for each”

An important yet often overlooked multiplicative idea is that of “for each”. It describes situations where every item or choice in one set is paired with every item or choice in another set. This structure lies at the heart of many mathematical ideas, including Cartesian product, which is the focus of this problem.
When students explore “for each” relationships, they begin to notice how numbers grow in a systematic way. For example, for each head in the flip book there are ten possible bodies, and for each of these, ten possible tails. Recognising this structure helps students see that multiplication represents repeated combinations rather than repeated addition.
Working with “for each” problems encourages students to move from counting individual outcomes to reasoning multiplicatively. Contexts such as the flip book make visible how multiplication can be used to represent all possible combinations.
An important yet often overlooked multiplicative idea is that of “for each”. It describes situations where every item or choice in one set is paired with every item or choice in another set. This structure lies at the heart of many mathematical ideas, including Cartesian product, which is the focus of this problem.
When students explore “for each” relationships, they begin to notice how numbers grow in a systematic way. For example, for each head in the flip book there are ten possible bodies, and for each of these, ten possible tails. Recognising this structure helps students see that multiplication represents repeated combinations rather than repeated addition.
Working with “for each” problems encourages students to move from counting individual outcomes to reasoning multiplicatively. Contexts such as the flip book make visible how multiplication can be used to represent all possible combinations.
Solving a simpler problem

A common strategy used by mathematicians to solve complex problems is to begin by breaking the problem down into a smaller, more manageable one. By exploring a simpler version, we can identify patterns, relationships, and structures that reveal how the problem works. This process helps us build understanding and make generalisations that can then be applied to the larger, complex problem.
In this sequence, students experience this way of thinking as they investigate the combinations in a flip book. Rather than tackling all possibilities at once, they might begin with just two heads, two bodies, and two tails. By representing and reasoning about this smaller problem, students notice the multiplicative structure. For each head there are several possible bodies, and for each of these, several possible tails. Once this structure is recognised, they can generalise to predict or calculate the total number of combinations in the full flip book.
This approach mirrors the work of mathematicians: starting small, looking for structure, and then generalising to develop a rule or relationship that applies more broadly. Through this process, students build confidence in reasoning, pattern-seeking, and generalisation, which are key practices at the heart of mathematical thinking.
A common strategy used by mathematicians to solve complex problems is to begin by breaking the problem down into a smaller, more manageable one. By exploring a simpler version, we can identify patterns, relationships, and structures that reveal how the problem works. This process helps us build understanding and make generalisations that can then be applied to the larger, complex problem.
In this sequence, students experience this way of thinking as they investigate the combinations in a flip book. Rather than tackling all possibilities at once, they might begin with just two heads, two bodies, and two tails. By representing and reasoning about this smaller problem, students notice the multiplicative structure. For each head there are several possible bodies, and for each of these, several possible tails. Once this structure is recognised, they can generalise to predict or calculate the total number of combinations in the full flip book.
This approach mirrors the work of mathematicians: starting small, looking for structure, and then generalising to develop a rule or relationship that applies more broadly. Through this process, students build confidence in reasoning, pattern-seeking, and generalisation, which are key practices at the heart of mathematical thinking.
Explain that the class will work together on a simpler problem by creating a human tree diagram with just two animals: the kookaburra and the platypus. Slides 3-13 of What is a Plocoroo? PowerPoint might be used to support this activity.
Working with the Animal cards, give the two head cards to two students and ask them to stand at the front of the room.
Ask: Working with just these two animals, how many body cards will be needed to show all the different combinations of heads and bodies?
Allow students to share their thinking and come to consensus as a class that four body cards will be needed to show all the different combinations of heads and bodies.
Hand out the four body cards and ask students to show all the combinations.
Ask: How many tail cards will be needed to show all the different combinations of heads, bodies and tails?
Again, allow students to share their thinking and come to consensus as a class that eight tail cards will be needed to show all combinations.
Hand out the eight tail cards and ask students to show all the combinations.
A tree diagram is a useful way to show all possible combinations in a Cartesian product problem. You could make this interactive by using string between students to represent the branches of the diagram.
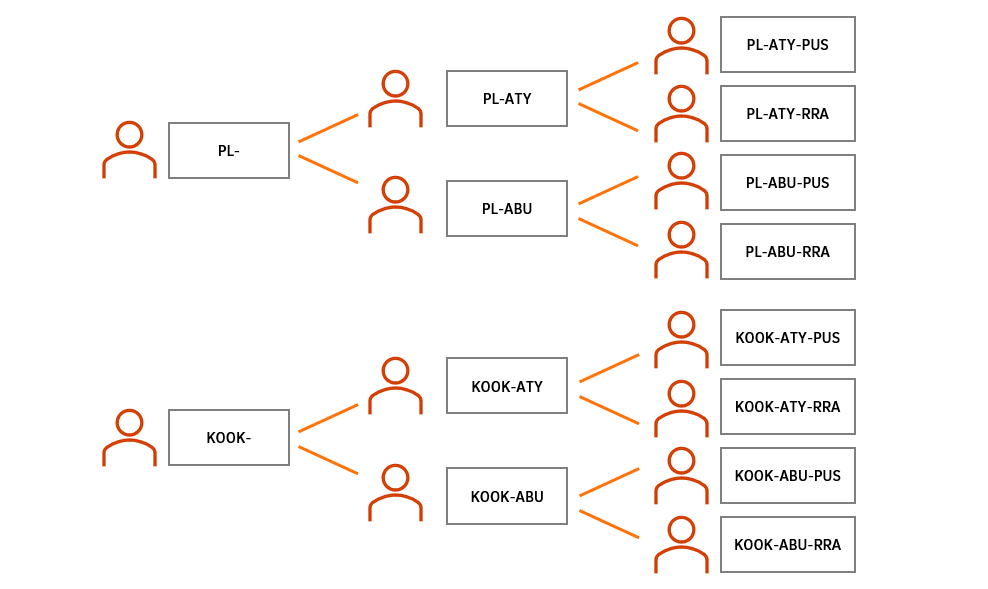
Allow students time to revisit their work and incorporate any new ideas or ways to represent their thinking.
Human tree diagram

A powerful way to make the multiplicative structure of “for each” visible to students is to involve them in creating a human tree diagram. This embodied approach allows students to physically experience the idea of “for each” and to see how the number of combinations increases systematically. By standing within the diagram, they can see and feel how each choice branches into further possibilities. This hands-on experience helps students move from concrete to abstract reasoning, prompting rich discussion about how many combinations are possible and why. It also supports them in noticing that the total number of combinations can be found by multiplying the number of options for each part.
The human tree diagram provides a shared visual and physical reference for later representations. Once students have built and counted combinations physically, they can record their thinking by constructing their own drawn tree diagrams.
A powerful way to make the multiplicative structure of “for each” visible to students is to involve them in creating a human tree diagram. This embodied approach allows students to physically experience the idea of “for each” and to see how the number of combinations increases systematically. By standing within the diagram, they can see and feel how each choice branches into further possibilities. This hands-on experience helps students move from concrete to abstract reasoning, prompting rich discussion about how many combinations are possible and why. It also supports them in noticing that the total number of combinations can be found by multiplying the number of options for each part.
The human tree diagram provides a shared visual and physical reference for later representations. Once students have built and counted combinations physically, they can record their thinking by constructing their own drawn tree diagrams.
Revisit slide 8 to 13 of What is a Plocoroo? PowerPoint to review the human tree diagram created by the class. Working with two animals, there were two heads. For each head, there were two possible bodies, and for each head-body combination, there were two tails—making eight possible animal combinations.
Discuss how the tree diagram clearly illustrates all possibilities and highlights the multiplicative structure of the problem. Note, however, that with ten animals the number of combinations becomes so large that a tree diagram is inefficient and impractical. Encourage students to look for relationships that can be generalised into more efficient strategies.
Invite selected students to present their solutions to the class. Include both those who solved simpler versions of the problem, and those who worked with all ten animals.
As students present, prompt the class to look for relationships.
Discuss:
- In the book What is a Plocoroo?, how many heads are there? For each head, how many bodies? For each body, how many tails?
- There are ten heads. For each head there are ten bodies, and for each body there are ten tails.
- How many combinations do you predict would be possible with two heads, three bodies and four tails? How do you know?
- 2 × 3 × 4 combinations will be possible, which is 24 animal combinations.
Invite students to share their predictions along with their reasoning, such as using skip counting or multiplication. Acknowledge their ideas but avoid confirming correctness at this stage as the multiplicative structure of the problem is the focus of the next task.
Noticing relationships, making generalisations

Mathematical thinking involves more than applying procedures—it requires students to notice relationships and connections between ideas. In this task, students explore how the number of animal parts (heads, bodies, and tails) and the total number of combinations are related multiplicatively. By paying attention to these relationships, students begin to see beyond individual calculations to the structure that underpins them. This shift, from simply counting or multiplying to recognising why multiplication applies, is fundamental to developing deeper conceptual understanding.
Noticing relationships lays the foundation for making generalisations. In this example, students first identify relationships within a smaller, more manageable problem and then generalise their thinking to a larger one. Task 2 provides an opportunity to test whether the relationship they have observed continues to hold true as the numbers and conditions change.
Noticing relationships and making generalisations help students move flexibly between focusing on individual parts and seeing how those parts connect to form a meaningful whole. This capacity to discern underlying structure and reason about general cases is a hallmark of mathematical thinking.
Mathematical thinking involves more than applying procedures—it requires students to notice relationships and connections between ideas. In this task, students explore how the number of animal parts (heads, bodies, and tails) and the total number of combinations are related multiplicatively. By paying attention to these relationships, students begin to see beyond individual calculations to the structure that underpins them. This shift, from simply counting or multiplying to recognising why multiplication applies, is fundamental to developing deeper conceptual understanding.
Noticing relationships lays the foundation for making generalisations. In this example, students first identify relationships within a smaller, more manageable problem and then generalise their thinking to a larger one. Task 2 provides an opportunity to test whether the relationship they have observed continues to hold true as the numbers and conditions change.
Noticing relationships and making generalisations help students move flexibly between focusing on individual parts and seeing how those parts connect to form a meaningful whole. This capacity to discern underlying structure and reason about general cases is a hallmark of mathematical thinking.
Explain that a tree diagram is useful for showing all possible combinations when the number of options is small. Point out that as the number of combinations grows, a tree diagram becomes inefficient, and a more efficient strategy is needed. Discuss how they should look for patterns and relationships to find and justify a more efficient strategy.
Revise: In the book, there were 10 heads. For each head there were 10 bodies, and for each body there were 10 tails. This means that 1000 different animals can be made.