Number: Taking handfuls
View Sequence overviewComparing allows us to order quantities and determine which quantity has more and which has less.
A common unit allows us to quickly compare quantities.
Whole class
A large quantity of small items which students can take a handful of (for example: counters, pasta, dried beans). A student handful should be around 10 to 20 items.
Each student
Comparing handfuls Student sheet
Task
Revise: In the last activity we learnt that some ways of arranging collections means that we can work out how many at a glance. We don't need to count! We also learnt that even though collections might be arranged differently, they can still have the same amount.
Pose the initial task: Take a handful and organise your collection in a way that makes it easy to see how many items are in your handful.
Allow students to count and organise their collections, then ask them to compare their organised handful with a partner.
Pose the question: Who has more and who has fewer items? It is likely that the students will have used different arrangements, which makes it more difficult to compare the two collections.
Pose the task: Take a new handful. Work with your partner to arrange your handfuls so it is easy to see how many there are in each handful, and to also see who has more and who has fewer.
Give students time to arrange their handfuls. As students are working, ask:
- How do your arrangements make it easy to see how many there are?
- How do your arrangements make it easy to see who has more and who has fewer items?
Provide students with the Comparing handfuls Student sheet. Ask students to record how they have arranged and compared their handfuls.
Both students in each pair need to arrange their items in the same way, using subitisable groups to easily see how many they have and to see who has more and who has fewer items.
- Students might make arrangements where it is easy to compare collections but not easy to see how many there are altogether. For example, making two lines of items (ensuring a common baseline and that there is one-to-one correspondence across the lines).
- Students might make arrangements where it is easy to see how many items are in each collection, but it is not easy to compare without counting. For example, using different arrangements of subitisable groups.
Allow students the chance to explore some of these options to determine if they can easily see how many and easily compare. Prompt students to think about how they might be able to arrange their collections so they can do both.
Making comparisons
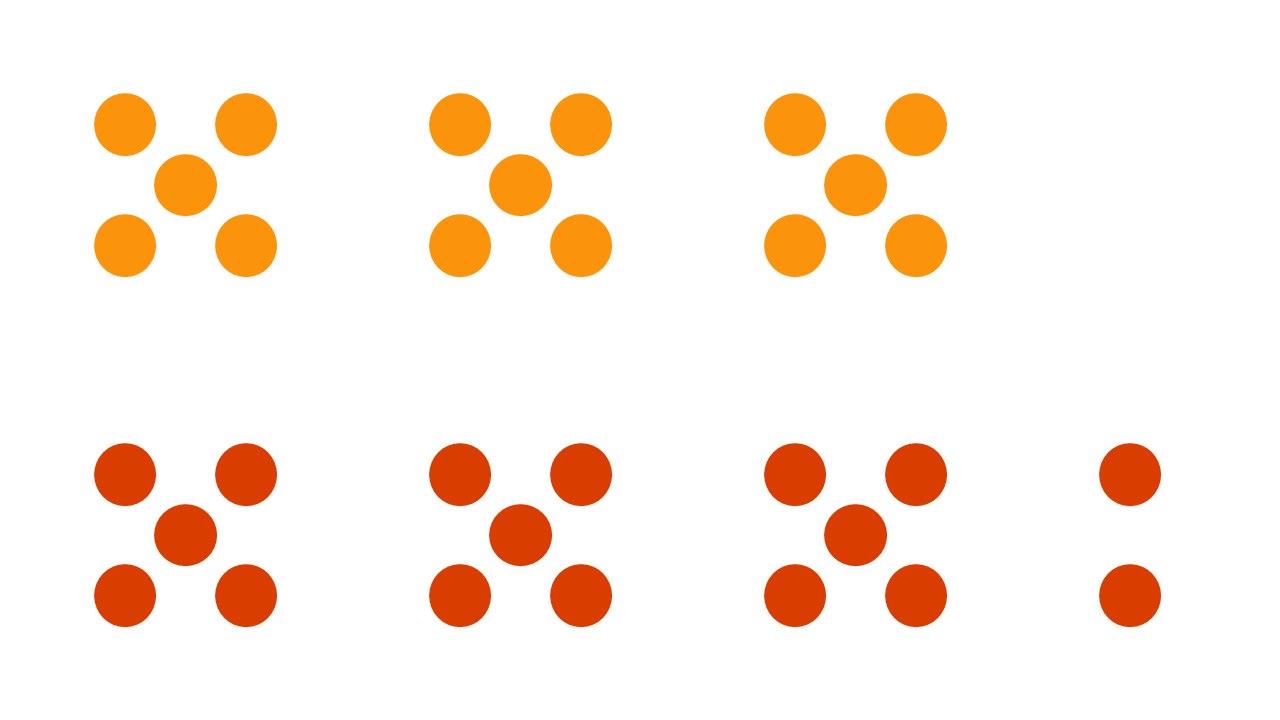
Up to this point in the sequence, students have been representing large collections using smaller subitisable sets so they can ‘see’ how many there are altogether. This task extends this idea of making smaller subitisable parts as a way to compare collections. When the same smaller subitisable sets are used across two collections, we can make quick visual comparisons.
Let’s use a collection of 15 and 17 as an example (see above). Both collections can be arranged using subitisable sets of 5. This makes it easy to see how many there are in each collection. It is also easy to see that 17 is two more than 15.
Up to this point in the sequence, students have been representing large collections using smaller subitisable sets so they can ‘see’ how many there are altogether. This task extends this idea of making smaller subitisable parts as a way to compare collections. When the same smaller subitisable sets are used across two collections, we can make quick visual comparisons.
Let’s use a collection of 15 and 17 as an example (see above). Both collections can be arranged using subitisable sets of 5. This makes it easy to see how many there are in each collection. It is also easy to see that 17 is two more than 15.
Review the original task (arrange your handfuls so it is easy to see how many there are in each handful, and to also see who has more and who has fewer items) and ask students to think about what they expect to see as they complete a gallery walk.
Ask students to consider the following questions as they look at others’ work: Look at how pairs of students have arranged their handfuls. Which arrangements make it easy to see how many there are and also to see who has more and who has fewer items? Why?
Conduct a class gallery walk.
Ask the students to return to their collections. Allow them to rearrange their items using the strategies they have seen, to make their collection easier to count and to see who has more and who has fewer items.
Learning from each other

Our purpose in using a gallery walk at this point in the task is not as a 'show-and-tell' activity, nor is it for students to look at others’ work and think about who has it 'right' or 'wrong'.
This gallery walk is designed to build students’ mathematical thinking skills. By looking at others’ work, students can critically reflect on how others have arranged their handfuls so they can compare quantities.
Remind students of the task and ask them to reflect on their own experience of doing the task before they commence the gallery walk. This helps to focus their attention on the mathematics they may expect to see. Provide students with time at the end of the gallery walk to alter their own solutions if they would like to. Students should not think of this as copying or cheating, rather they are learning from their peers.
Our purpose in using a gallery walk at this point in the task is not as a 'show-and-tell' activity, nor is it for students to look at others’ work and think about who has it 'right' or 'wrong'.
This gallery walk is designed to build students’ mathematical thinking skills. By looking at others’ work, students can critically reflect on how others have arranged their handfuls so they can compare quantities.
Remind students of the task and ask them to reflect on their own experience of doing the task before they commence the gallery walk. This helps to focus their attention on the mathematics they may expect to see. Provide students with time at the end of the gallery walk to alter their own solutions if they would like to. Students should not think of this as copying or cheating, rather they are learning from their peers.
There are two important ideas to bring out in this Connect phase:
- Arranging counters in subitisable groups makes it easy to see how many there are in a collection.
- A common unit makes it easy to compare collections to see which has more and which has less.
Discuss:
- Which arrangements made it easy to see how many counters there were? Why?
- Subitising patterns (such as those on dice) make it easy to see at a glance how many items are in an arrangement.
- Which arrangements made it easy to see who had more and who had fewer counters? Why?
- A common unit is needed for quick comparison. For example, making a line of counters (ensuring a common baseline and that there is one-to-one correspondence across the lines) uses the common unit of ‘one’.
- Were there any arrangements that made it easy to see how many there are and also to see who had more? Why?
- The best way to do this is to use the same subitisable patterns. Students can quickly see how many they have and also who has more.
Ask the students to return to their collections. Again, provide time to rearrange the counters if they would like to. Ask students to record their new arrangements of their handfuls on their student sheet.
Discuss with the students whether they found it easier to compare their collections this time. Ask students how they arranged their collections in similar ways to make comparing easier.
Explain: Comparing allows us to see who has more and which has less. Arranging our collections in the same way makes it easier to compare.