Number: Margot’s macaroni
View Sequence overviewA number line is a useful tool for representing and comparing quantities.
Whole class
Margot’s macaroni PowerPoint
Display of student hand cut-outs from the previous task
Adult-sized hand cut-out with 100 written in the middle
Sticky notes to create the class number line
Masking tape (if creating a number line on the floor)
Each group
Bag or tub of small macaroni pieces. Ensure the macaroni pieces are small enough for students to grab a handful containing 100 pieces.
At least 12 sticky notes or small cards
1 sticky note or card marked with 100
Task
Revise: We have learnt that we can quickly count our handfuls by organising the macaroni pieces into equal groups. Doing this means we do not have to count every piece one by one.
Allow students to share efficient counting strategies that they used.
Show the students slide 5 of Margot’s macaroni PowerPoint.
Continue the story:
Last night, I rang Grandma to explain the problem with my soup. I told her that we thought that the handful of macaroni might have been the problem. My handful could have been different to her handful.
I asked her how big her handful was, and she said that her handful had 100 pieces of macaroni.
Ask: Did anyone have the same number as Grandma Margot?
Refer to the ordered line of hands from the previous lesson. Use an adult-sized cut-out hand labelled 100 to represent Grandma’s handful and, as a class, decide where it fits.
Use the ordered hands to decide which handfuls are closest in size to Grandma’s. Students may assume that the hands directly beside Grandma’s show the numbers closest to 100. However, they may not recognise that “closeness” is determined by relative distance from 100, not simply by position in the order. For example, in the sequence 92, 95, 100, 102, and 104, the numbers 102 and 104 are closer to 100 than 95 and 92. Also note whether students understand that a number greater than 100 can be closer than a number less than 100.
Pose the challenge: I wonder if we can grab a handful of 100 macaroni pieces, like Grandma? We will need to efficiently count the number of macaroni pieces in our handful to see if we have 100.
Pose the questions: How can we grab a handful with 100 macaroni pieces, just like Grandma’s? How can we quickly check if our handful has 100 pieces?
Explain to students that these questions will guide the investigation.
Divide students into small groups of 3-4 students. Provide each group with a bag/tub of small macaroni pieces and at least 12 sticky notes/cards.
Ask students to each take a handful of macaroni, to count their handful using efficient strategies, and then write the total in their handful on a sticky note/card, along with their name or initials.
Allow time for all students to count and record the total for at least two handfuls.
Observe how students are counting and if they are employing the efficient strategies discussed in the previous lesson. Ideally students should be creating groups of twos, fives, or tens. Take note of the following:
- Are the groups equal in size? Prompt students to consider how to ensure each group has the same number.
- Are they using skip counting to find the total, or still counting by ones? Ask how the group structure could support more efficient counting.
- Are the groups organised to facilitate efficient counting? Arranging groups into subitisable or recognisable structures makes it easier to see at a glance how many items are in each group. Some pieces may not fit into a complete group. Prompt students to think about how to handle these extras.
Provide each group with a sticky note/card marked 100 to represent Grandma Margot’s handful. Ask groups to order their handful totals, along with the sticky note/card marked 100, in ascending order. Once ordered, have each group discuss and reach consensus on which handful is closest to 100 and which is second closest. Each group member should also decide which of their handfuls is closest to 100.
Observe students ordering their sticky notes/cards and strategies they use to determine which numbers are closest to 100.
- When ordering the numbers, do the students start with the smallest number first and then look for the second smallest? Challenge the students to use 100 as a reference point. Ask: Which number/s will come before 100 and which number/s will come after 100? Order the numbers around 100.
- Do students use 100 as a reference point? Do students place the numbers more randomly, positioning them approximately and then rearranging as needed? Using 100 as a benchmark and closely approximating the relative position of numbers demonstrates strong number sense.
- Do students accurately determine which handfuls are closest to 100? Observe whether they recognise that ‘closeness’ is determined by the relative distance from 100, not simply by position in the order. For example, in the sequence 92, 95, 100, 102, and 104, the numbers 102 and 104 are closer to 100 than 95 and 92. Also note whether students understand that a number greater than 100 can be closer than a number less than 100.
Building on collective experience

In the previous task, the class ordered the numbers on the hand cut-outs from smallest to largest. At the beginning of this lesson, students worked together to identify which of these numbers were closest to 100.
Both activities were carried out as whole-class experiences, carefully guided by the teacher. Rather than telling students how to order the numbers, the teacher remained responsive to their thinking and reasoning, using their ideas as a springboard to highlight important mathematical concepts and model sound reasoning.
Following these whole-class experiences, students work in small groups to apply their understanding. This phase is intentionally designed to build on the shared class experiences and the teacher’s modelling.
In the previous task, the class ordered the numbers on the hand cut-outs from smallest to largest. At the beginning of this lesson, students worked together to identify which of these numbers were closest to 100.
Both activities were carried out as whole-class experiences, carefully guided by the teacher. Rather than telling students how to order the numbers, the teacher remained responsive to their thinking and reasoning, using their ideas as a springboard to highlight important mathematical concepts and model sound reasoning.
Following these whole-class experiences, students work in small groups to apply their understanding. This phase is intentionally designed to build on the shared class experiences and the teacher’s modelling.
Ask each group to bring to the floor the sticky note showing the total of the handful closest to 100, as well as the one that was second closest. Place a sticky note labelled with 100 on the board or in an open space on the floor.
Ask a member from each group to place their two sticky notes/cards in order, using 100 as a reference point.
Ask: Whose handful is closest to Grandma’s handful?
Discuss as a class which handfuls are closest to 100. Consider the numbers before and after 100.
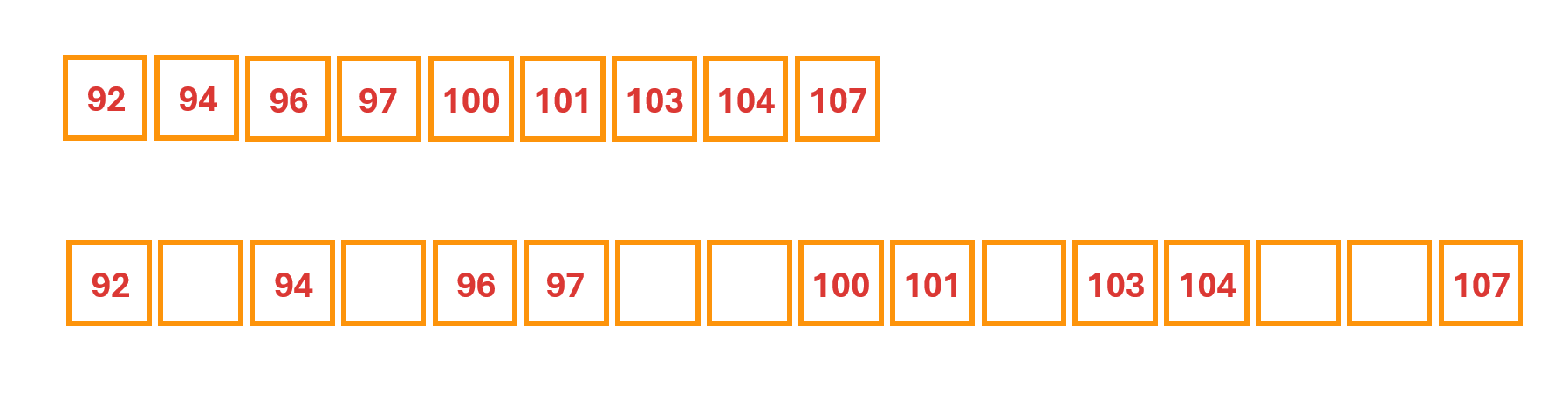
Explain that it is difficult to see at a glance which numbers are closest to 100 just by ordering the numbers. Discuss that some numbers are missing, and spaces have not been left for the missing numbers. Create a number line to indicate the position of the numbers in relation to 100.
Use evenly spaced blank sticky/notes cards to represent any missing numbers between the smallest and largest numbers on the number track.
If working on the board, draw a line above the numbers; if working on the floor, create a line with masking tape. Extend the line beyond the first and last numbers, so that it runs through the smallest and largest handfuls. Mark each number with a small tick on the line to show its position, gradually building a number line. Add ticks for numbers that come between those currently shown. Finally, remove any blank cards.
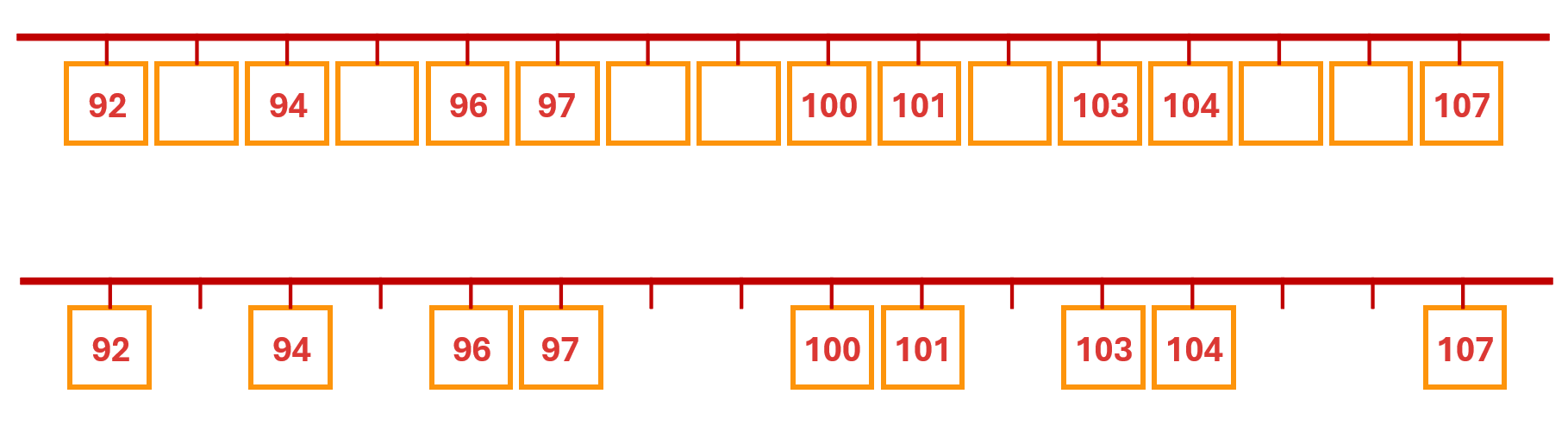
If you created the number line on the floor, transfer it to the wall for use in the following lesson.
Ask students if it is easier to see which numbers are closest to 100 now.
Invite students to collect all of their sticky notes/cards and place their handfuls in the correct position on the number line. Numbers can be placed in a line underneath each other where there are duplicates.
Number lines

Representations are essential for explaining and communicating mathematical structure and relationships. A number line is a visual representation that extends infinitely in both directions and helps students develop number sense and understand numerical relationships. Its effective use requires intentional teaching to ensure students understand what the number line represents and how to interpret it.
In this context, the number line allows students to represent the number of macaroni pieces in their handful, compare the size of their handful to those of their peers and to Grandma’s, and engage in meaningful discussions about the relative magnitude of numbers.
Representations are essential for explaining and communicating mathematical structure and relationships. A number line is a visual representation that extends infinitely in both directions and helps students develop number sense and understand numerical relationships. Its effective use requires intentional teaching to ensure students understand what the number line represents and how to interpret it.
In this context, the number line allows students to represent the number of macaroni pieces in their handful, compare the size of their handful to those of their peers and to Grandma’s, and engage in meaningful discussions about the relative magnitude of numbers.
Conduct a class discussion.
Discuss:
- What was the smallest handful? What was the largest handful?
- Look at the smallest and largest handfuls. You might consider which of these numbers is closest to 100.
- Who got close to Grandma Margot’s handful of 100 macaroni pieces?
- Look at the numbers that are closest to 100, even if they are slightly above it. Some students may not realise that a number greater than 100 can still be the closest.
- Which made it easier to compare the size of handfuls, the ordered cards or the number line? Why?
- The number line clearly shows distance between the numbers, which is not apparent with the ordered cards.
Talk moves—revoicing

Talk moves are teacher strategies that support meaningful discussion and help students express and build on mathematical thinking.
In this discussion, have a go at using “revoicing”. Revoicing is a talk move that helps clarify meaning, highlight key ideas, or reveal misunderstandings. When the teacher revoices a student’s response, it refocuses attention on the learning goal and gives students another opportunity to hear, see, and connect important ideas.
It is even more powerful to ask one or even two students to revoice what was said by another student. This ensures that the idea is heard more than once, supports active listening, and helps build individual and collective understanding.
Talk moves are teacher strategies that support meaningful discussion and help students express and build on mathematical thinking.
In this discussion, have a go at using “revoicing”. Revoicing is a talk move that helps clarify meaning, highlight key ideas, or reveal misunderstandings. When the teacher revoices a student’s response, it refocuses attention on the learning goal and gives students another opportunity to hear, see, and connect important ideas.
It is even more powerful to ask one or even two students to revoice what was said by another student. This ensures that the idea is heard more than once, supports active listening, and helps build individual and collective understanding.
Discuss how a number line represents the position of numbers and is useful for comparing quantities because it shows the distance between numbers, not just their order.
Explain: We can use a number line to show the position of numbers and to compare them. A number line doesn’t just tell us the order, it also shows the distance between numbers.