Lesson 5 • How far our frogs jump

Show students slide 11 of the Origami frogs PowerPoint which presents the PPDAC statistical investigation process.

Revise: We have our problem to investigate: How far can an origami frog jump?. We made a plan, represented our data, and analysed our data. Now we can conclude the investigation by answering our question.

Show the students the data display saved from the previous lesson. As a class, use the data to answer the question about how far an origami frog can jump. Discuss what is more likely to be the length of a frog jump, and is less likely, but still possible.

Explain to students that everyone will make a new frog and that these frogs will be used in a frog jump-off. Provide the students with new origami or construction paper and ask them to fold a frog.

Set up a jumping arena with a common starting line (about 1m long) that has been marked with masking tape. Divide students into small groups and explain that the groups will take turns to jump their frogs in the arena. Explain that before groups jump their frogs they need to predict how far they think the frogs might jump. Discuss with students that predictions should include:

• words such as likely or unlikely when making predictions as we cannot know for certain what will happen.
• evidence from the data to justify the prediction.

In turn, invite groups of 5-6 students into the arena with their frogs. Ask students around the outside (audience) to make their predictions to a classmate and then ask the competitors to jump their frogs. Measure each frog jump and record the length of the jump on a sticky note and stick it next to the frog in the area. Examine the data display made by the frogs. Discuss whether the predictions made by the audience were close to the final results.

Transfer the sticky notes to the board and add them to the class data display created in the previous lesson. This new data will extend beyond the current hat plot that has been marked.

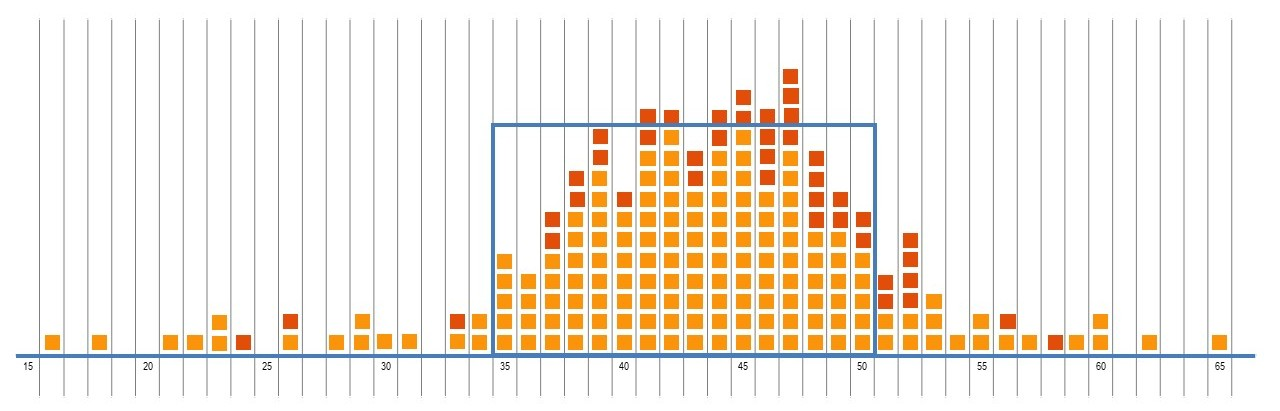
Continue the jump off until all students have had at least two turns of being a competitor.

Conduct a class discussion:

• The crown of a hat plot indicates the data that is in the centre. It is about the middle half of our data. Now that we have this new data, should we adjust the crown and the brim of our hat plot? 
  • It is likely that the new data means that the centre looks different. Adjust the crown and brim as needed.
  • Discuss how the shape of the data has changed.

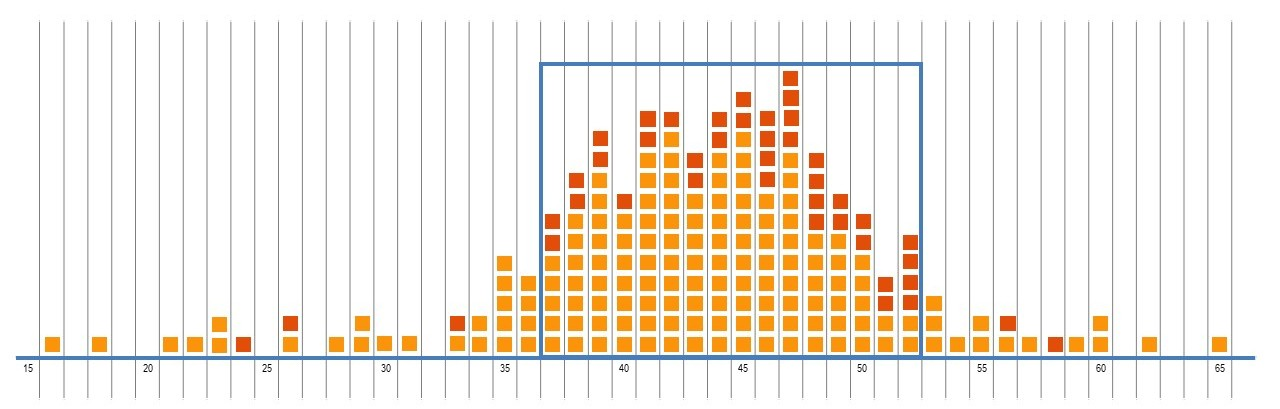
• If I jumped my frog now, how far do you think it might jump? How is you prediction this time different to your prediction at the start of this lesson.
  • With the additional data, students may make predictions that are more defined, that is that cover a smaller range of data. The more data, the crown of the hat plot (that is, the centre of the data), may become more defined and less spread.

Conduct a final jump-off between the frogs that jumped the furthest. The frog that jumps furthest on this jump is crowned the winner.