Multiplication: reSolve Market
View Sequence overviewThe array is a powerful representation of the ‘how many groups’ and ‘how much in each group’ structure of multiplication.
Whole class
reSolve Market PowerPoint
Each group
Blank A3 paper
Counters
Each student
Fruit arrays Sheet
Task
Use the reSolve Market PowerPoint to continue the context of the reSolve Market.
Revise: Multiplication is based on equal-sized groups. These might be represented as groups or as an array in rows and columns. In multiplication, we need to work out two things: ‘how many groups’ and ‘how much in each group’.
Show students slide 6.
I have been looking very closely at this picture and I have noticed some similarities between the different examples of multiplication that we have found.
Show slide 7. This slide has been divided into four sections. Each section has two pictures of fruit which are related.
Here are some examples of similarities that I found.
Pose the question: How are these different examples similar?
Provide each student with an A3 sheet of paper and a copy of Fruit arrays Sheet.
Have students work with a partner or in small groups. Ask them to create a poster on their A3 paper of the similarities and differences they notice between the two displays of fruit in each section. Students should record this information in any way they choose including using materials, diagrams, cut-up fruit arrays, numbers, and equations.
This task asks students to notice the connections between the two displays of fruit in each section. In particular, take note of whether students use the language of ‘how many groups’ and ‘how much in a group’ to explain the relationships that they notice. For example:
- The limes and pears are similar because they are both arranged into 3 groups with 5 in each group. They are different because the limes are in 3 bags of 5 and the pears are in 3 rows of 5.
Consider: Do students notice connections between the number of smaller arrays of mangoes and the whole mango array?
- How are the pairs of pictures similar and how are they different?
- What do you notice about how the fruit is organised? Describe any ways that you notice it has been grouped.
- How many mangoes are in each part? How can you be sure without counting them all?
- How could the mangoes help you to find the number of apples?
- How could the mangoes be partitioned in a different way again?
Talking about multiplication

We have suggested working in pairs or small groups during the Explore phase of this task to promote mathematical discourse. Mathematical talk in the classroom is fundamental to both knowing and doing mathematics. Students should have regular opportunities to work on and talk about solving problems in community with peers.
It is likely that each student in the group will approach the task in slightly different ways. Through discourse, students put forth claims and justify them as well as listening to and critiquing claims of others. Solving problems in community provides a venue for more talking and listening than is available when working individually or in a teacher-led lesson.
We have suggested working in pairs or small groups during the Explore phase of this task to promote mathematical discourse. Mathematical talk in the classroom is fundamental to both knowing and doing mathematics. Students should have regular opportunities to work on and talk about solving problems in community with peers.
It is likely that each student in the group will approach the task in slightly different ways. Through discourse, students put forth claims and justify them as well as listening to and critiquing claims of others. Solving problems in community provides a venue for more talking and listening than is available when working individually or in a teacher-led lesson.
Use the illustrations on slides 6 and 7 of reSolve Market PowerPoint to support the discussion.
Select some students to present their work to the class, particularly noting the way that they represented and recorded the relationships that they noticed.
Slides 8, 9, 10 and 11 represent each collection of fruit using an equation, in the form:
$$ \text{how many groups} \times \text{how much in a group} = \text{the total in the group}$$
Discuss: How are the two fruit displays similar? How are they different? The similarities between the fruit on each slide is clearly evident in the equations:
- The mangoes and apples and the limes and pears are represented using the same equation.
- The oranges are an example of the communitive property. We can see that one fact can be turned around to make another fact.
- For each type of berry, the number of groups (punnets) increases by one each time.
Understanding the relationships


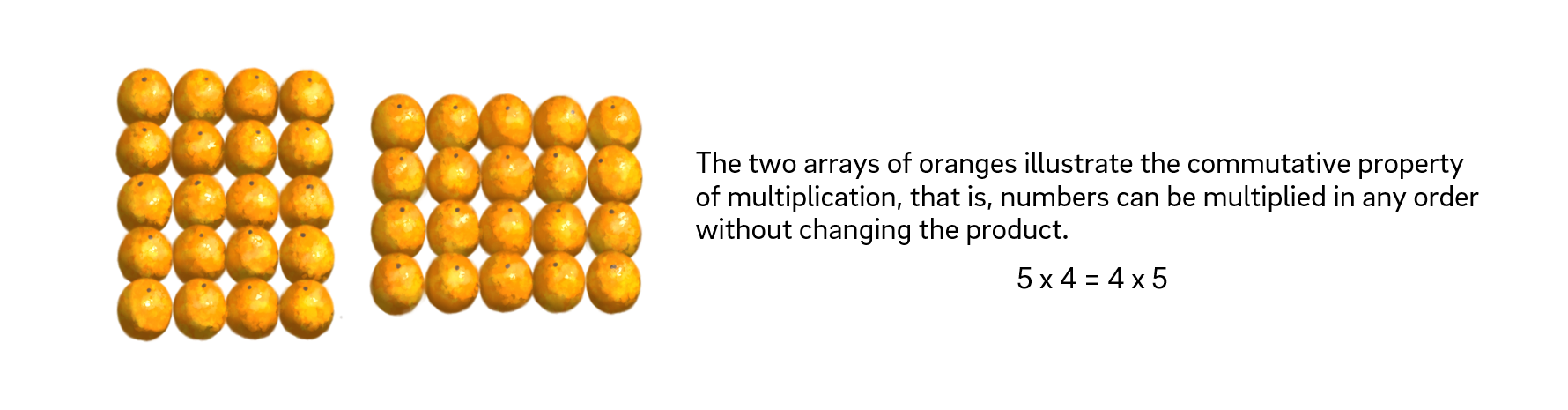



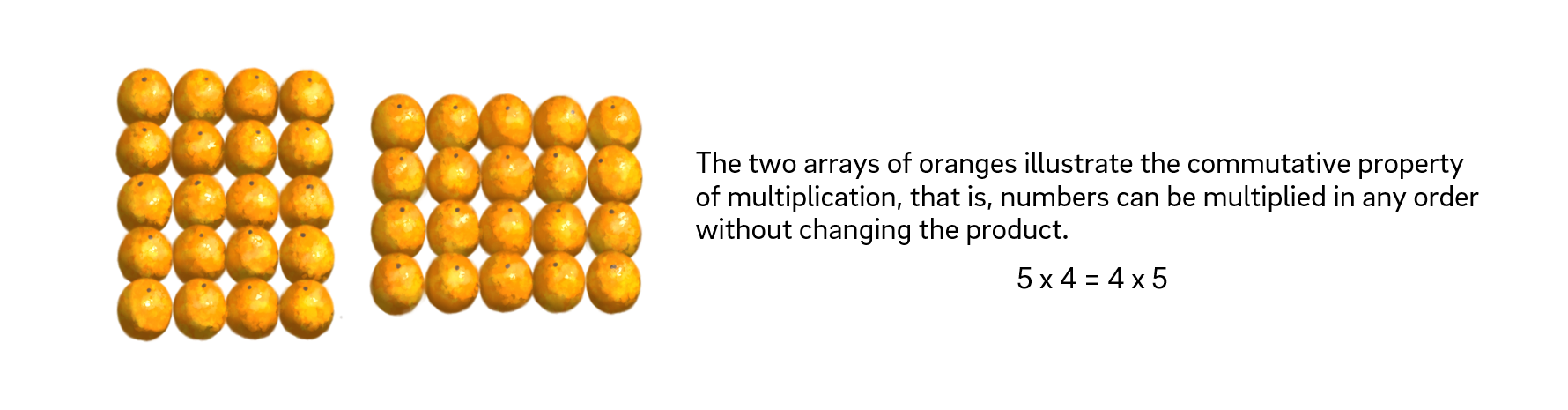


Introducing multiplication equations

Multiplication is a complex operation. Students have to keep track of two things:
- how many groups
- how much in each group
This double count can be made explicit for students by the teacher using a numeral when you record how many and a word when you record how much.
4 groups with 6 in each group are 4 sixes
It can also be recorded as a multiplication fact:
$$\text{how many} \times \text{how much} = \text{the whole}$$
The array is a powerful tool for modelling how many and how much. The count of how many indicates the number of rows and the count of how much indicates the number in each row.
Multiplication is a complex operation. Students have to keep track of two things:
- how many groups
- how much in each group
This double count can be made explicit for students by the teacher using a numeral when you record how many and a word when you record how much.
4 groups with 6 in each group are 4 sixes
It can also be recorded as a multiplication fact:
$$\text{how many} \times \text{how much} = \text{the whole}$$
The array is a powerful tool for modelling how many and how much. The count of how many indicates the number of rows and the count of how much indicates the number in each row.
Explain: The array is a very helpful representation for multiplication. We can clearly see ‘how many groups’ and ‘how much in each group’. In the reSolve Market we can use how many and how much to look for relationships between the different fruit displays.
Discuss how identifying how many and how much helped us to see relationships between the different fruit displays.
Add this new understanding to the class display along with students’ work samples.
Class display

In the Summarise phase, the following statement is presented to students:
The array is a very helpful representation for multiplication. We can clearly see ‘how many groups’ and ‘how much in each group’. In the reSolve Market we can use how many and how much to look for relationships between the different fruit displays.
This statement reflects the learning goal for the task and is the understanding that we want all in the class to share. As the sequence progresses, this shared understanding is built on.
Add to the class display created in Task 1. Create a banner or poster of this shared understanding and include an illustration of the array. Display the students’ work samples underneath or around the shared understanding. This provides the opportunity for students to revisit and reflect on this understanding and the ways that that it is reflected in the different solutions strategies used by students. The display is a way to help ensure the understanding is truly shared by all in the class.
Presenting everyone’s work with this statement communicates that everyone has contributed to and participated in developing this understanding as shared in the class, regardless of how complex or sophisticated their thinking may or may not be.
In the Summarise phase, the following statement is presented to students:
The array is a very helpful representation for multiplication. We can clearly see ‘how many groups’ and ‘how much in each group’. In the reSolve Market we can use how many and how much to look for relationships between the different fruit displays.
This statement reflects the learning goal for the task and is the understanding that we want all in the class to share. As the sequence progresses, this shared understanding is built on.
Add to the class display created in Task 1. Create a banner or poster of this shared understanding and include an illustration of the array. Display the students’ work samples underneath or around the shared understanding. This provides the opportunity for students to revisit and reflect on this understanding and the ways that that it is reflected in the different solutions strategies used by students. The display is a way to help ensure the understanding is truly shared by all in the class.
Presenting everyone’s work with this statement communicates that everyone has contributed to and participated in developing this understanding as shared in the class, regardless of how complex or sophisticated their thinking may or may not be.