Multiplication: reSolve Market
View Sequence overviewRelated multiplication and division facts can be found in the array. These related facts are known as a fact family.
Whole class
reSolve Market PowerPoint
Each group
Counters
Each student
Lemon arrays Student sheet
Limes and kiwifruit arrays Student sheet
Task
Use reSolve Market PowerPoint to continue the context of the reSolve Market. Show slide 27.
Revise: We have learnt that we can calculate the whole by multiplying how many rows/groups by how much is in each row/group.
Show slide 28. Ask: How many lemons are there? How could we work it out?
- This is a quick revision question to see if the students know to multiply 4 by 6. If students do not know the answer, they can share how they might work it out.
Continue the context:
The grocer wishes to take the lemons out of the bags and arrange all of them in an array like the oranges, apples, peaches, apricots and mangoes. She wants to make one array with more than one lemon in each row and column.
Pose the task: How could the grocer arrange all the lemons in just one array? Can you find more than one way?
Provide students with Lemon arrays Student sheet. Also provide them access to counters to use if they choose.
Allow students time to explore the problem. For each array that they find, they should record on their student sheet a diagram of the array and the corresponding multiplication fact.
As there needs to be more than one lemon in each row and column, there are six possible ways to arrange 24 lemons:
- 2 rows of 12 and 12 rows of 2
- 3 rows of 8 and 8 rows of 3
- 4 rows of 6 and 6 rows of 4
Ask: How do you know you have found them all? Can you see similarities between the arrays?
Observe whether students are applying the understandings developed through this sequence, including:
- Do the students use equal rows and columns to create their arrays?
- Are they able to use a multiplication fact to represent each array?
- Do they recognise that they can use the commutative property of multiplication to record two different options?
- Which numbers cannot be used for the number of rows in your array?
- There are quite a few numbers it is not possible to use to make an array for 24. This prompts students to start eliminating possibilities and thinking more systematically.
- Have you found all possible answers?
- Working systematically helps find all possibilities. For example:
- One lemon in each row is not allowed (according to the question).
- Two lemons in each row creates a 2 x 12 array.
- Three in each row creates a 3 x 8 array.
- Four in each row creates a 4 x 6 array, and so on.
- Working systematically helps find all possibilities. For example:
- Which arrangement do you think will work best in the fruit shop? Why?
- There is no right answer for this question, but students should consider the different shapes and sizes of the arrays.
The array
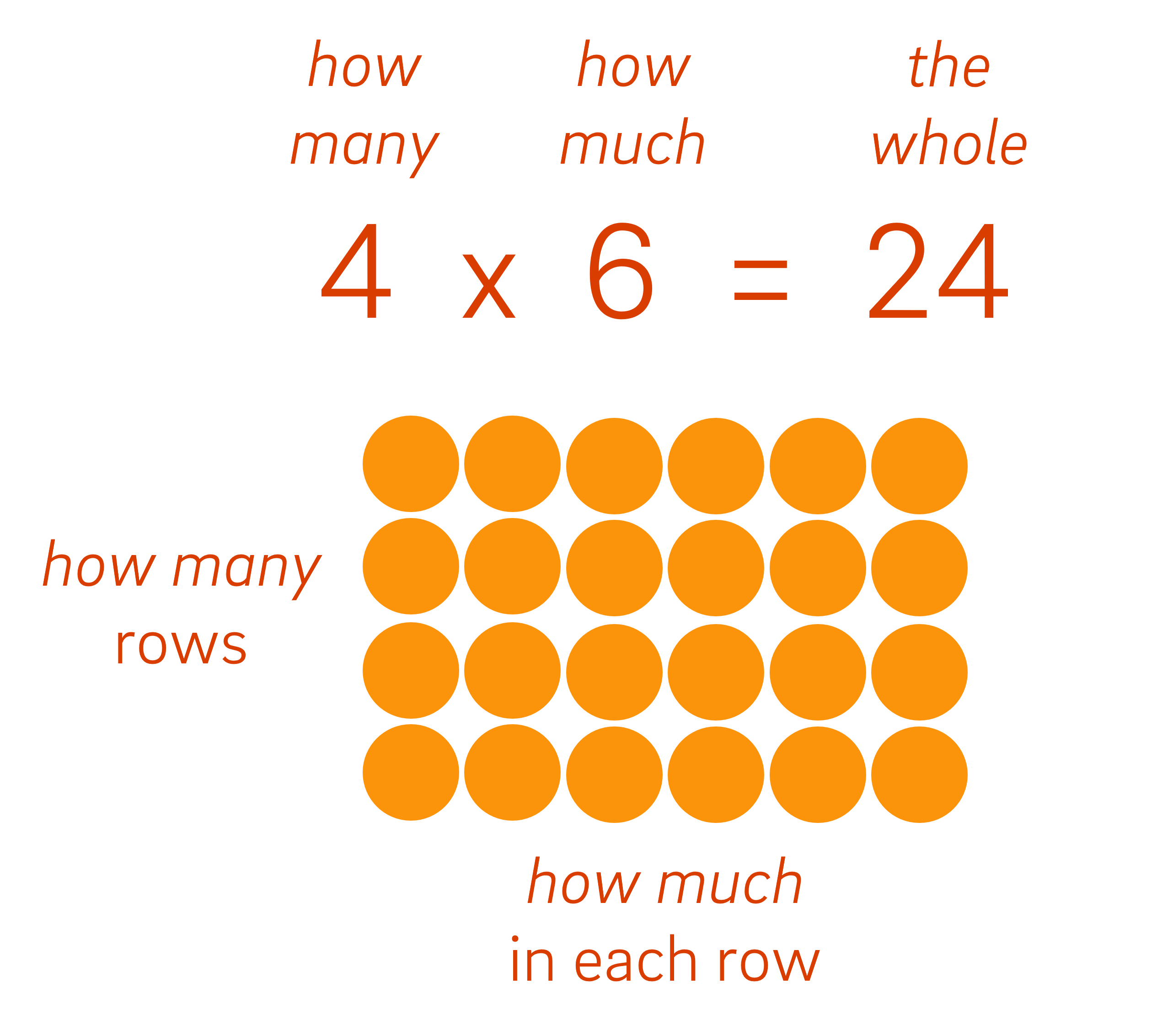
The array provides a structure for thinking about equal groups which makes the connections between the groups and the whole visible. Specifically, the structure of the array highlights the relationship that exists between:
- the whole (product)
- how many rows/groups (first factor)
- how much in each row/group (second factor)
The array provides a structure for thinking about equal groups which makes the connections between the groups and the whole visible. Specifically, the structure of the array highlights the relationship that exists between:
- the whole (product)
- how many rows/groups (first factor)
- how much in each row/group (second factor)
Invite some students to share the different solutions that they found with the class. Record the different solutions that students found on the board in no particular order.
Ask: Have we found all possible answers? How will we know if we have found them all?
Working systematically helps find all possibilities. For example:
- One lemon in each row is not allowed (according to the question).
- Two lemons in each row creates a 2 x 12 array.
- Three in each row creates a 3 x 8 array.
- Four in each row creates a 4 x 6 array.
- Five in each row does not create an array.
- Six in each row creates a 6 x 4 array.
- Seven in each row does not create an array.
- Eight in each row creates an 8 x 3 array, and so on.
Show slide 29 of reSolve Market PowerPoint.
4 bags of lemons with 6 lemons in each bag can be arranged into a 4 x 6 array. It can also be divided into 3 x 8 array.
We know that we can represent this as $4 \times 6$ and $3 \times 8$.
Discuss: What other facts can we see from these arrays?
- This question introduces fact families. Four related facts are evident in the array (or two facts for square numbers). It also highlights the inverse nature of multiplication and division.
- For the 4 x 6 array we can see $4 \times 6$, $6 \times 4$ (the commutative property), $24 ÷ 4 = 6$ and $24 ÷ 6 = 4$.
- For the 3 x 8 array we can see $3 \times 8$, $8 \times 3$ (the commutative property), $24 ÷ 3 = 8$ and $24 ÷ 8 = 3$.
- Read the Fact families professional learning embedded in this step to learn more about the importance of using fact families when teaching multiplication and division.
Show slide 30 and 31.
Look at the how the two multiplication and the two division facts can be seen in the one array.
Explain: We can see four different facts from the one array. Once we know one fact, we actually know four!
Show slide 32.
The grocer wants to take the limes and kiwifruit out of their bags as well. She wants to arrange the limes in an array like the oranges, apples, peaches, apricots and mangoes. She also wants to arrange the kiwifruit in an array.
Pose the task: How could the grocer arrange all the limes in just one array? How could the grocer arrange all the kiwifruit in just one array? Can you find all the fact families for each array?
Provide students with Limes and kiwifruit arrays Student sheet. Also provide them access to counters to use if they choose.
Allow students time to explore this second problem. This time the focus is not on finding many arrays, but on recording the fact family for any array that is found. For each array that students find they should record a diagram of the array and the corresponding fact family.
Introducing division

There is an inverse relationship between multiplication and division. Students have learnt that you can find the whole by multiplying how many and how much. In this task, students learn that that dividing the whole by how many will give how much, or that that dividing the whole by how much will give how many.
Coordinating the three quantities, the whole, how many, and how much allows a family of facts to be derived from one fact. For example, knowing the first multiplication fact generates this fact family:
$$4 \times 6 = 24$$
$$6 \times 4 = 24$$
$$24 ÷ 6 = 4$$
$$24 ÷ 4 = 6$$
There is an inverse relationship between multiplication and division. Students have learnt that you can find the whole by multiplying how many and how much. In this task, students learn that that dividing the whole by how many will give how much, or that that dividing the whole by how much will give how many.
Coordinating the three quantities, the whole, how many, and how much allows a family of facts to be derived from one fact. For example, knowing the first multiplication fact generates this fact family:
$$4 \times 6 = 24$$
$$6 \times 4 = 24$$
$$24 ÷ 6 = 4$$
$$24 ÷ 4 = 6$$
Invite some students to share the different arrays that they found for the limes and the kiwifruit. Record the array and the fact family for each array on the board.
Explain: We can see four different facts from the one array. Once we know one fact, we actually know four!