Statistics: Loopy aeroplanes
View Sequence overviewWe use data as evidence to inform predictions about what is likely and to answer questions.
Whole class
Loopy aeroplanes PowerPoint
Each group
4 sticky notes: 2 of one colour, 2 of a different colour
Loopy aeroplanes made in previous lessons
Various tools used for measuring distance such as tape measures, metre rulers, and trundle wheels
Lesson
Provide each group with four sticky notes, two notes in one colour and two in a different colour. On the first two sticky notes, students write the distance of the two throws with the small loop at the front. On the second two sticky notes, students write the distance of the two throws with the large loop at the front.
Have students stick their sticky notes randomly onto the board.
Discuss:
- We have all of our data up on the board. Now can we answer which design is best?
- This will be a mess of data, and it will be very hard to make predictions or draw conclusions using the data. Establish the need to organise and represent the data in a way that it makes it easier to analyse.
- How might we organise and represent this data so that it is easier to analyse?
- Follow students’ suggestions. If students suggest sorting the sticky notes into two groups according to the two different designs, follow their directions and discuss if the data is easy to compare and analyse. Establish the need for all data to be organised on one common representation to allow comparison.
Discuss with students how graphs are one helpful way to represent and see patterns in data. Create a dot plot using the sticky notes on the board. An example dot plot is shown below.
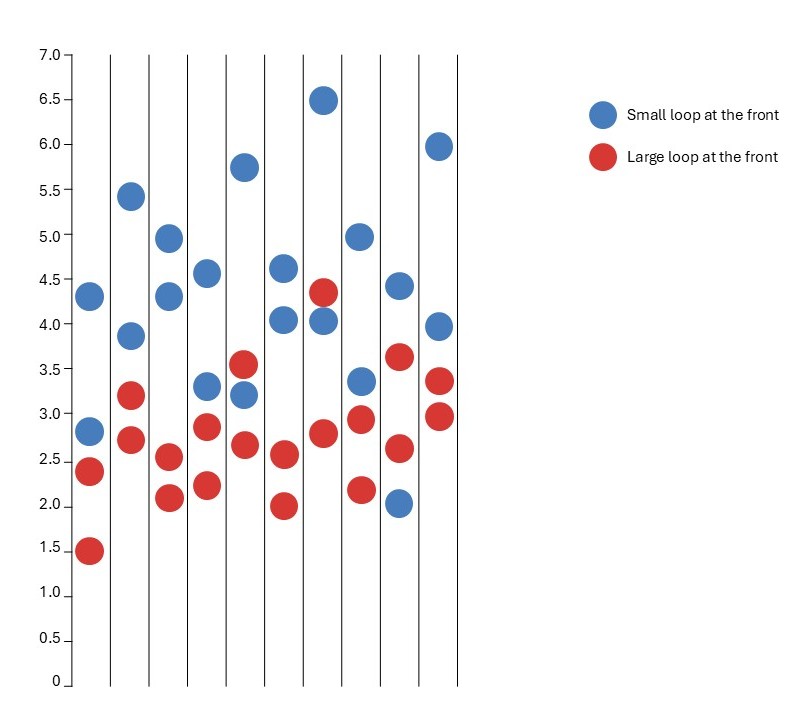
Dot plots

A dot plot is a simple representation consisting of data points plotted as dots on a graph with an x- and y-axis.
In this case, the groups are represented on the x-axis, and the y-axis represents distance travelled. “Dots” in this instance are sticky notes and represent each loopy aeroplane throw. The dots are placed on the graph according to group and distance travelled.
A dot plot is a simple representation consisting of data points plotted as dots on a graph with an x- and y-axis.
In this case, the groups are represented on the x-axis, and the y-axis represents distance travelled. “Dots” in this instance are sticky notes and represent each loopy aeroplane throw. The dots are placed on the graph according to group and distance travelled.
Discuss with the students what they notice about the data display. As students make claims or predictions, make sure they use evidence from the data to support their claims and predictions.
Discuss:
- What do you notice from the data?
- Most of the planes with the small loop at the front went further than the large loop planes.
- Can we say for certain that flying the plane with the small loop at the front will always go further than flying the plane with the large loop at the front?
- It is likely that some throws with the large loop at the front went further than some throws with the small loop at the front. It is important that observations are expressed as likelihoods rather than certainties, such as “when the small loop is at the front the plane is likely to fly further”.
- If I threw my loopy aeroplane with the small loop first, how far do you predict it will go? What if I threw it with the large loop first? How far do you predict it will go?
- Make sure students use evidence from the data to support their predictions. These questions can be answered using a precise measurement (e.g. 3.4m) or using a range (3-6m). Discuss with students that answering with a range allows a more reasonable prediction to capture the variability in flight distance.
Revise the throwing and measuring protocols and return to an open space. Allow the students to test their predictions about how far their planes will fly with the different loops at the front of the plane. Take the time to converse with different groups of students, asking:
- How far do you predict your plane will fly with the small/large loop at the front? What makes you say that?
- As students collect more data, their predictions are likely to change. The greater volume of data may mean their predictions will become more accurate.
- Do you predict that when the small loop is at the front your plane will always fly further?
- The data indicates that it is “likely” that the plane will fly further with the small loop at the front, however it is not certain. The use of conditional language is important.
Take a photo of the class dot plot for use in Lesson 7.
Making predictions

Prediction is a natural part of life. Statistics provides a set of highly effective concepts, tools, practices and dispositions to strengthen our capacity to make predictions.
Students’ predictions on how far their plane might fly are much more than just a wild guess. Their predictions are based on evidence from the data that they have collected.
When making their predictions, students are making a claim beyond what is currently known. This means that our predictions should be expressed with uncertainty and provide supporting evidence for the claim. For example, “I think that the plane with the small loop at the front will probably go about 5m because most planes of this design went close to this distance.” In this statement, uncertainty is expressed through the use of the words “probably” and “about”. The evidence used to support this claim is that “most planes of this design went close to this distance”.
Prediction is a natural part of life. Statistics provides a set of highly effective concepts, tools, practices and dispositions to strengthen our capacity to make predictions.
Students’ predictions on how far their plane might fly are much more than just a wild guess. Their predictions are based on evidence from the data that they have collected.
When making their predictions, students are making a claim beyond what is currently known. This means that our predictions should be expressed with uncertainty and provide supporting evidence for the claim. For example, “I think that the plane with the small loop at the front will probably go about 5m because most planes of this design went close to this distance.” In this statement, uncertainty is expressed through the use of the words “probably” and “about”. The evidence used to support this claim is that “most planes of this design went close to this distance”.