Place value: What’s in a number?
View Sequence overviewThe position of a digit in a number gives it its unit value.
A digit represents the number of units in a place value position.
A number is the sum of its unit values.
Whole class
What’s in a number? PowerPoint
Each group
Venn diagram place value sort cards, cut into cards
Place value sort Game Board printed on A3 paper and laminated for future use
Build
Revise: In the previous task we found that some numbers can belong to more than one group when we sort using place value.
Show slide 13 of What’s in a number? PowerPoint.
Ponder: I wonder what Hugo did to sort these numbers?
Allow students time to discuss the ways that the numbers have been sorted and why there are numbers in the overlap/intersection.
Invite students to share their thinking and discuss:
- How have the numbers in each group been sorted? Explain your thinking.
- What is the rule for each group?
- What’s the connection between the numbers in the overlap/intersection?
- What other numbers would fit in each circle? Explain your thinking.
Show slide 14.
Ponder: I wonder what Kayla was thinking when she sorted these numbers? Discuss.
Show slide 15.
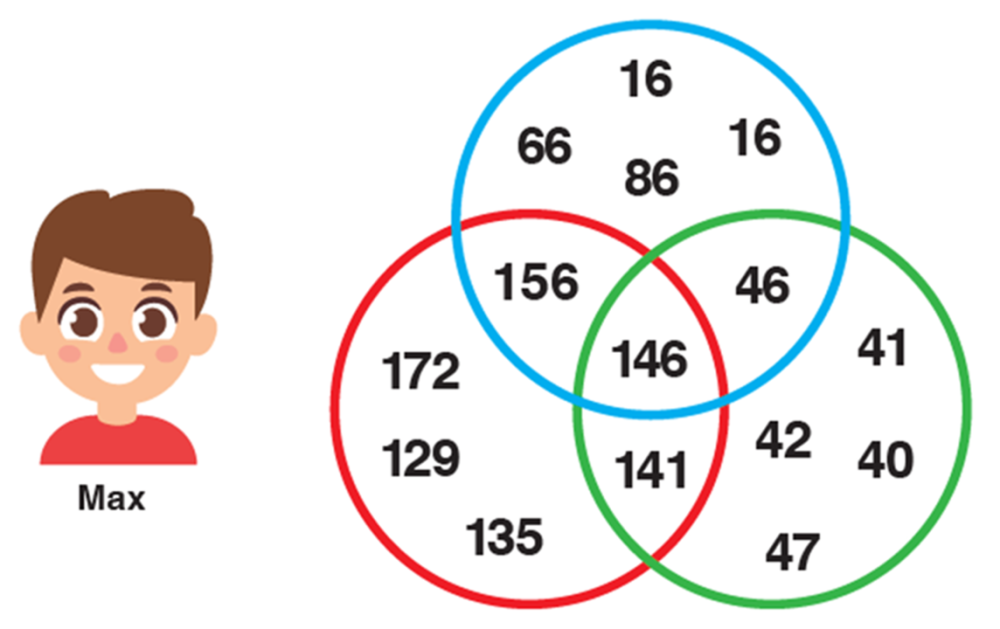
Ponder: How did Max use place value to sort these numbers?
Allow students time to discuss the ways that Max's numbers have been sorted and the connections between the numbers in the overlaps/intersections.
Show slide 16-19 of What’s in a number? PowerPoint to deconstruct the Venn diagram into each circle for students to see each separate sort.
Invite students to share their thinking and discuss:
- What place value ideas have been used to sort numbers into groups? Explain your thinking.
- What’s the connection between the numbers in the overlaps/intersections and each individual circle? Explain your thinking.
- What other numbers would fit in each circle? Explain your thinking.
Using the Venn diagram as a thinking tool
The Venn diagram model is used as a purposeful learning tool to engage students in deeper reflection on place value properties. It provides a clear visual structure that supports students in organising their thinking and making sense of numerical relationships.
In this task, the Venn diagram enables students to systematically compare and contrast the properties of numbers represented in each circle, while simultaneously analysing the number(s) located in the intersection. Students are prompted to consider why certain numbers belong exclusively to one group, why others belong to both, and how the intersecting number(s) demonstrate shared place value characteristics. This process draws attention to both similarities and differences and encourages students to look beyond individual numbers to identify underlying patterns and relationships.
By making these relationships explicit and visible, students are supported in recognising common place value structures and forming generalisations about how numbers are composed. Through discussion, justification, and reflection, students refine their understanding of place value concepts, revise misconceptions, and extend their mathematical thinking.
The Venn diagram model is used as a purposeful learning tool to engage students in deeper reflection on place value properties. It provides a clear visual structure that supports students in organising their thinking and making sense of numerical relationships.
In this task, the Venn diagram enables students to systematically compare and contrast the properties of numbers represented in each circle, while simultaneously analysing the number(s) located in the intersection. Students are prompted to consider why certain numbers belong exclusively to one group, why others belong to both, and how the intersecting number(s) demonstrate shared place value characteristics. This process draws attention to both similarities and differences and encourages students to look beyond individual numbers to identify underlying patterns and relationships.
By making these relationships explicit and visible, students are supported in recognising common place value structures and forming generalisations about how numbers are composed. Through discussion, justification, and reflection, students refine their understanding of place value concepts, revise misconceptions, and extend their mathematical thinking.
Revise: We know we can sort numbers using place value and thinking about the number of hundreds, the number of tens and the number of ones. We can sort in ways so that some numbers belong in more than one group.
Slides 21-23 of What’s in a number? PowerPoint show the place value sort cards, the place value game board and rules for how to play, if you choose to use these with students.
Model how to play Place value sort for the whole class, prior to students playing in pairs:
- Shuffle the Venn diagram place value sort cards and place them face down in a pile next to the Place value sort Game Board.
- One player draws a card from the pile and places it in the centre intersection of the Venn diagram on the game board.
- Each player thinks of a place value rule for one of the Venn diagram circles, making sure their rule applies to the number in the intersection. They record their rule next to the circle.
- Players take turns drawing a card and put it in the appropriate place on the game board. If the card does not fit in either circle, they can place the card next to the board.
- The game ends when all cards have been placed.
When the game ends, players can shuffle the cards and play again with a different number card in the intersection.
Optional: Players may make their own number cards to add to the game to increase the challenge.