Multiplication: Trays of arrays
View Sequence overviewWhen multiplying two numbers, if we divide one number by four and multiply the other number by four the product remains the same. Equivalence in multiplication is maintained no matter how the numbers are grouped.
Whole class
Trays of arrays PowerPoint
Each group
Trays of cupcakes picture, printed on A4 and cut in half
Blank A3 paper
Task
Use Trays of arrays PowerPoint to continue the context of the reSolve Bakery. Show students the illustration of the bread rolls on slide 23.
Revise: Halving one number and doubling the other number in a multiplication problem maintains equivalence.
Show the picture of the baker and cakes on slide 24.
The baker bakes three trays of cupcakes each day which are packed into boxes. There are two dozen cupcakes on each tray. These cupcakes need to be packed into boxes of six cupcakes ready to sell.
The baker remembers that when he was packing the bread rolls, he needed twice the number of bags as there were trays. “I have three trays of cakes so I will need six boxes to pack all the cakes”.
Show the picture of the second cupcake array on slide 25.
Pose the task: Does the baker have the right number of boxes to pack all the cakes?
Revision
You might choose to use equations as you revise the learning from the previous task. Below is an example of what you might do.
There were 5 trays of bread rolls with 12 on each tray.
$$5 \times 12$$
To pack the bread rolls into bags of 6 we halved the 12 rolls on one tray to make 2 groups of 6 bread rolls.
$$5 \times (2 \times 6)$$
We found that on each tray there were enough bread rolls for two bags. This meant that there were double the number of bags as trays.
$$(5 \times 2) \times 6$$
So, we halved the 12 to make 2 groups of 6 bread rolls on each tray, which meant that there were double the number of bags as trays.
$$5 \times (2 \times 6) = (5 \times 2) \times 6$$
You might choose to use equations as you revise the learning from the previous task. Below is an example of what you might do.
There were 5 trays of bread rolls with 12 on each tray.
$$5 \times 12$$
To pack the bread rolls into bags of 6 we halved the 12 rolls on one tray to make 2 groups of 6 bread rolls.
$$5 \times (2 \times 6)$$
We found that on each tray there were enough bread rolls for two bags. This meant that there were double the number of bags as trays.
$$(5 \times 2) \times 6$$
So, we halved the 12 to make 2 groups of 6 bread rolls on each tray, which meant that there were double the number of bags as trays.
$$5 \times (2 \times 6) = (5 \times 2) \times 6$$
Provide each pair with a sheet of A3 paper and access to Trays of cupcakes picture to use if they choose.
Allow students time to investigate the problem and to present their solution as a poster on the A3 paper.
Through the investigation, students will realise that six boxes will not be enough to pack all the cakes. Ask them to work out how many boxes the baker will need to pack all the cakes into boxes of six.
How do students divide the cakes into boxes of six? Do students:
- Share by ones: Prompt students to consider what they learnt from the previous task to help them complete this task.
- Create groups of six: When students have made the groups of six, remind them of the previous task and the relationships that were evident. Ask them to look at the numbers in this problem and consider if there are similar relationships that exist.
- Use the relationships between the numbers: Ask the students to record the relationships that they see using words and/or numbers, and to explain why these relationships exist.
- Why is it not twice as many boxes as trays this time?
- There are 24 cakes on each tray which means that there are enough cakes on each tray to pack six full boxes.
- What is the relationship between the numbers in the problem? Why does this relationship exist?
- This time four boxes of six can be made from one tray of cakes. That means we will need four times as many boxes as trays. The relationship is a multiplicative one: by dividing 24 into four groups of six, you need to multiply the number of trays by four to determine the total number of boxes needed.
- How many boxes of six cakes will you be able to make from four trays of 18? Can you work out a way to quickly calculate a solution to the problem?
- This question prompts the students to think more deeply about the multiplicative relationship between the numbers and how this relationship can be used to calculate the number of boxes needed.
- 18 can be divided into three groups of six. You need to multiply four (the number of trays) by three to determine the total number of boxes needed.
Work samples
Look at how these students have solved the problem.
Discuss with colleagues: What do these students know and what have they shown that they can do? Give evidence from the pictures for your statements.
Look at how these students have solved the problem.
Discuss with colleagues: What do these students know and what have they shown that they can do? Give evidence from the pictures for your statements.
Mathematical talk
We have suggested working with in pairs or small groups during most Explore phases in this sequence. Working with others promotes mathematical discourse which is fundamental to both knowing and doing mathematics. Students should have regular opportunities to work on and talk about solving problems in community with peers. It is likely that each student in the group will approach the task in slightly different ways. Through discourse, students put forth claims and justify them as well as listening to and critiquing claims of others. Solving problems in community provides a venue for more talking and listening than is available when working individually or in a teacher-led lesson.
We have suggested working with in pairs or small groups during most Explore phases in this sequence. Working with others promotes mathematical discourse which is fundamental to both knowing and doing mathematics. Students should have regular opportunities to work on and talk about solving problems in community with peers. It is likely that each student in the group will approach the task in slightly different ways. Through discourse, students put forth claims and justify them as well as listening to and critiquing claims of others. Solving problems in community provides a venue for more talking and listening than is available when working individually or in a teacher-led lesson.
Invite some students to share their solutions with the class. Consider how the different strategies are different and how they are similar.
Record the solution to the problem on the board in the following way:
3 trays of 24
12 boxes of 6
Discuss:
- What relationships do you notice?
- The number of boxes is four times the number of trays, and the number of cakes in a box is a quarter of the number on a tray.
- Why do these relationships exist?
- The cakes on one tray are packed into four boxes. Each tray of cakes is divided into four smaller groups of six. This means we need four times the number of boxes as trays.
Explain to students that we can make sense of this relationship using the array and numbers. Show students Trays of arrays PowerPoint slides 26 and 27. These slides illustrate how the associative property applies to this task.
Discuss how the array helps to make sense of these relationships and that equivalence in multiplication is maintained no matter how the numbers are grouped.
Associative property of multiplication
The associative property of multiplication states that the multiplication of a set of numbers gives the same output no matter how the numbers are grouped. So,
$$(a \times b) \times c = a \times (b \times c)$$
Let’s see how this property applies to this problem.
There are 3 trays of cakes with 24 on each tray.
$$3 \times 24$$
The 24 cakes on one tray can be divided into 4 groups of 6. This creates 3 trays of bread rolls with 4 groups of 6 on each tray.
$$3 \times (4 \times 6)$$
There are 3 trays, and each tray has enough cakes for 4 bags. There are 6 cakes in each box.
$$(3 \times 4) \times 6$$
We divide the 24 into 4 groups of 6 cakes on each tray. This means that there are 4 times the number of boxes as trays.
$$3 \times (4 \times 6) = (3 \times 4) \times 6$$
The associative property of multiplication states that the multiplication of a set of numbers gives the same output no matter how the numbers are grouped. So,
$$(a \times b) \times c = a \times (b \times c)$$
Let’s see how this property applies to this problem.
There are 3 trays of cakes with 24 on each tray.
$$3 \times 24$$
The 24 cakes on one tray can be divided into 4 groups of 6. This creates 3 trays of bread rolls with 4 groups of 6 on each tray.
$$3 \times (4 \times 6)$$
There are 3 trays, and each tray has enough cakes for 4 bags. There are 6 cakes in each box.
$$(3 \times 4) \times 6$$
We divide the 24 into 4 groups of 6 cakes on each tray. This means that there are 4 times the number of boxes as trays.
$$3 \times (4 \times 6) = (3 \times 4) \times 6$$
Noticing relationships
“Noticing” is the active process of attending to and make sense of mathematical patterns and relationships. We want students to “notice” the relationships between the numbers in this task. We also want students to explain why the relationships in this task are different to the relationships that we noticed in the previous task when we were packing bread rolls.
Encourage students to use different forms of representation to explain the relationships that they see. For example, they might use the array, words, and symbols (such as equations or expressions) to explain these relationships.
“Noticing” is the active process of attending to and make sense of mathematical patterns and relationships. We want students to “notice” the relationships between the numbers in this task. We also want students to explain why the relationships in this task are different to the relationships that we noticed in the previous task when we were packing bread rolls.
Encourage students to use different forms of representation to explain the relationships that they see. For example, they might use the array, words, and symbols (such as equations or expressions) to explain these relationships.
Use Trays of arrays PowerPoint slide 27 to review the learning from this task.
Review: To find how many boxes of cakes there would be we divided the 24 into four groups of six, which we represented as $4 \times 6$. We had three trays and there were enough cakes on each tray to pack four boxes with six cakes. So, to find the number of boxes there would be we multiplied three by four to make 12, which we represented as $3 \times 4$.
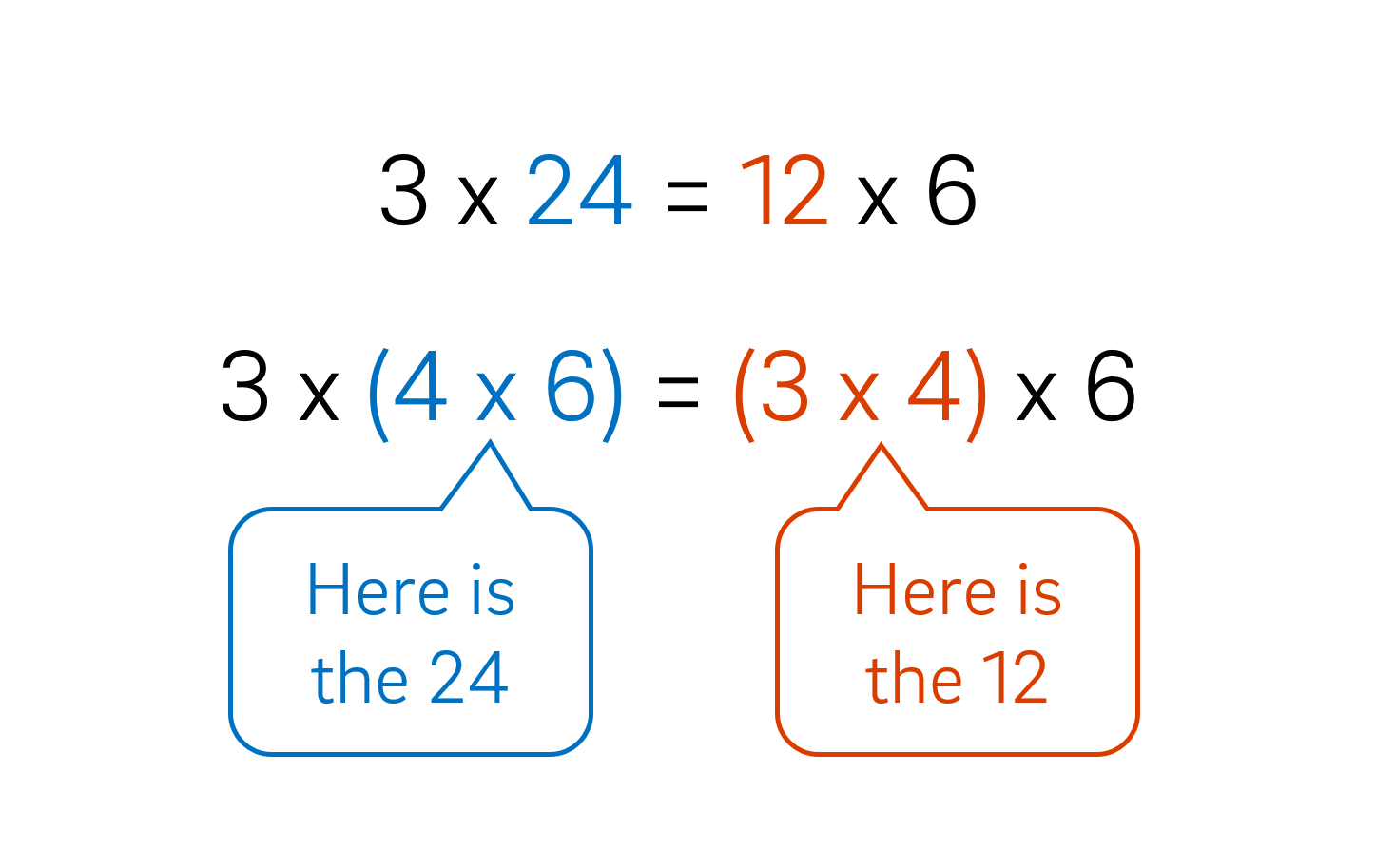
On one side of the equation the 4 was grouped with the 6 and on the other side the 4 was grouped with the 3.
Explain: Equivalence in multiplication is maintained no matter how the numbers are grouped. This helps us understand why, when we multiply two numbers, we can divide one number by four and multiply the other number by four to ensure the total remains the same.
Add to the class display using the students' posters from this task, using the summary statement from above as a title for the display. Read the Class display professional learning embedded in this step to learn how this display can be used to build a shared understanding amongst the students.
Class display
The statement presented in this Summarise phase is the shared understanding that we want for all students in the class.
Extend the class display of work to include this Summarise statement and students work samples. This provides the opportunity for students to revisit and reflect on this understanding and the ways that that it is reflected in the different solutions strategies used by students. The display is a way to help ensure the understanding is truly shared by all in the class. Students can also see how their shared understanding is developing through the sequence.
Presenting everyone’s work with this statement communicates that everyone has contributed to and participated in developing this understanding as shared in the class, regardless of how complex or sophisticated their thinking may or may not be.
The statement presented in this Summarise phase is the shared understanding that we want for all students in the class.
Extend the class display of work to include this Summarise statement and students work samples. This provides the opportunity for students to revisit and reflect on this understanding and the ways that that it is reflected in the different solutions strategies used by students. The display is a way to help ensure the understanding is truly shared by all in the class. Students can also see how their shared understanding is developing through the sequence.
Presenting everyone’s work with this statement communicates that everyone has contributed to and participated in developing this understanding as shared in the class, regardless of how complex or sophisticated their thinking may or may not be.