Multiplication: Trays of arrays
View Sequence overviewIn multiplication, factors can be partitioned and distributed to make partial products. The partial products are then added together to find the product of the original multiplication (distributive property).
When multiplying a set of numbers, the product is the same no matter how the numbers are grouped.
Whole class
Trays of arrays PowerPoint
Each group
Set of Card Sort cards, printed on A4 and then cut out
Template for students to make their own Card Sort
Build
Use Trays of arrays PowerPoint to review the learning so far in this sequence.
Show slide 35.
Revise: We can solve a difficult multiplication problem by partitioning factors to create smaller problems. The products of these smaller problems are then added together to find the find the product of the original problem.
Show slide 36.
Revise: We also learnt that when multiplying a set of numbers, the product is the same no matter how the numbers are grouped. This helps us understand why, when multiplying two numbers, halving one number means we need to double the other number to ensure the total remains the same. Or dividing one number by four and multiplying the other number by four to ensure the product remains the same.
Explain to students that they will be matching equations with corresponding array representations and that the learning just revised will help the students complete the task.
Provide pairs of students with a Set of Card Sort cards and ask them to create matching pairs of equations and arrays.
Allow time for students to complete the activity, then bring students together for a whole class discussion. Show slide 37 from Trays of arrays PowerPoint.
Discuss: In the card sort, $7 \times 8$ was solved three different ways. Which strategy would you use? Why? The focus here is on which strategies are most efficient. For example, students may reason that $(5 \times 8) + (2 \times 8)$ is an easier calculation to perform as compared to $7 \times 2 \times 2 \times 2$ or $(7 \times 5) + (7 \times 3)$, as the answer to $5 \times 8$ is a whole ten, which makes it easy to add on the $2 \times 8$.
Ask students to review each question in their Set of Card Sort cards and decide which strategy they think is the most efficient.
Distributive property of multiplication
Students are asked to partition the array into smaller parts to solve this problem. They are being asked to apply the distributive property of multiplication. The distributive property is a fundamental arithmetic property of our number system.
In multiplication, numbers can be partitioned and distributed to make partial products. The partial products are then added together to find the original total of the multiplication. This is known as the distributive property of multiplication.
This can be expressed algebraically as:
$$a (b + c) = (a \times b) + (a \times c)$$
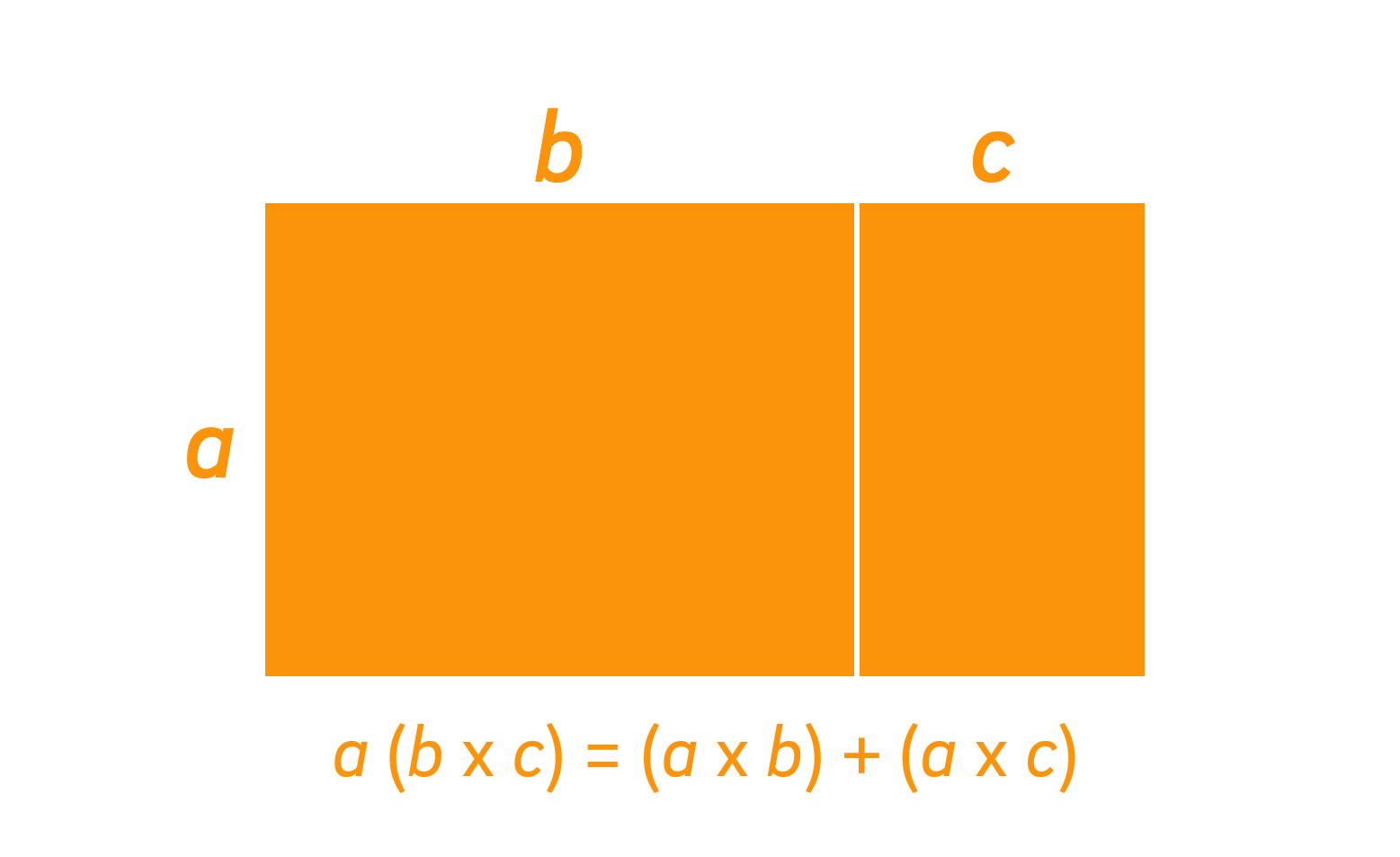
Let’s consider the distributive property applied to $12 \times 4$:
12 can be partitioned into $10 + 2$. Each part is then multiplied by 4. The partial products formed are then added together to find the total.
This can be represented using following equation:
$$12 \times 4 = (10 \times 4) + (2 \times 4)$$
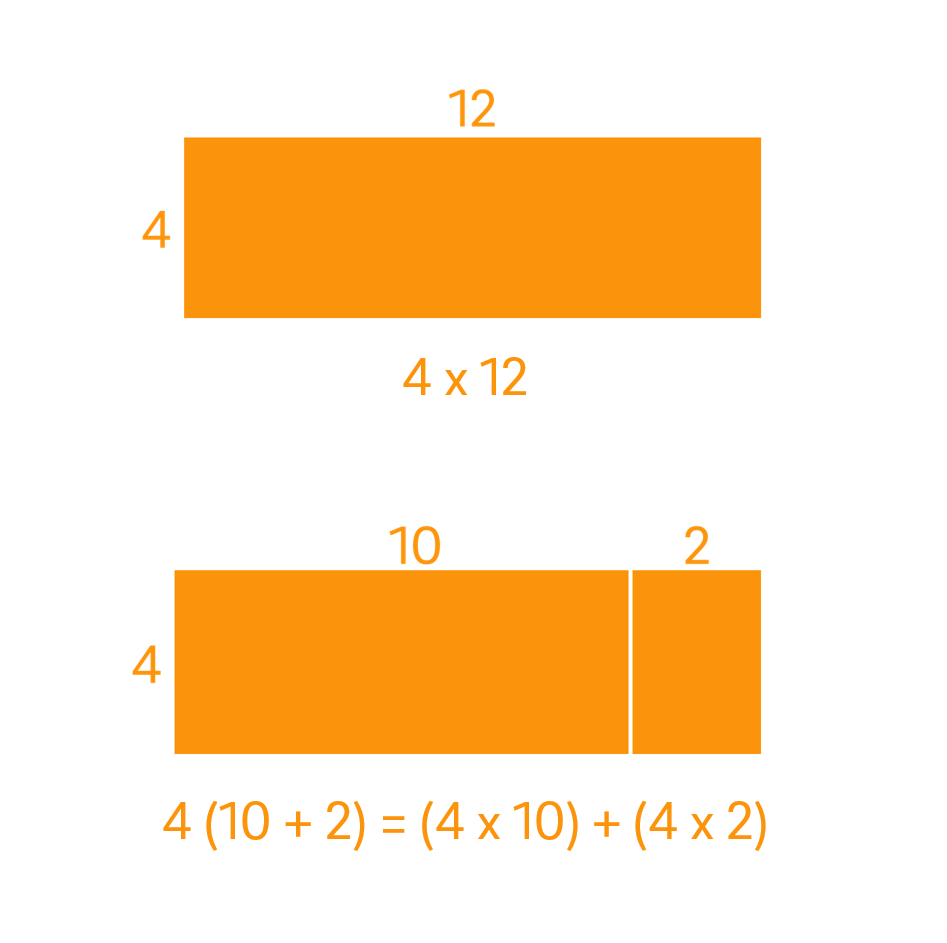
It is called the distributive property because the 4 is distributed across the 10 and the 2.
Students are asked to partition the array into smaller parts to solve this problem. They are being asked to apply the distributive property of multiplication. The distributive property is a fundamental arithmetic property of our number system.
In multiplication, numbers can be partitioned and distributed to make partial products. The partial products are then added together to find the original total of the multiplication. This is known as the distributive property of multiplication.
This can be expressed algebraically as:
$$a (b + c) = (a \times b) + (a \times c)$$
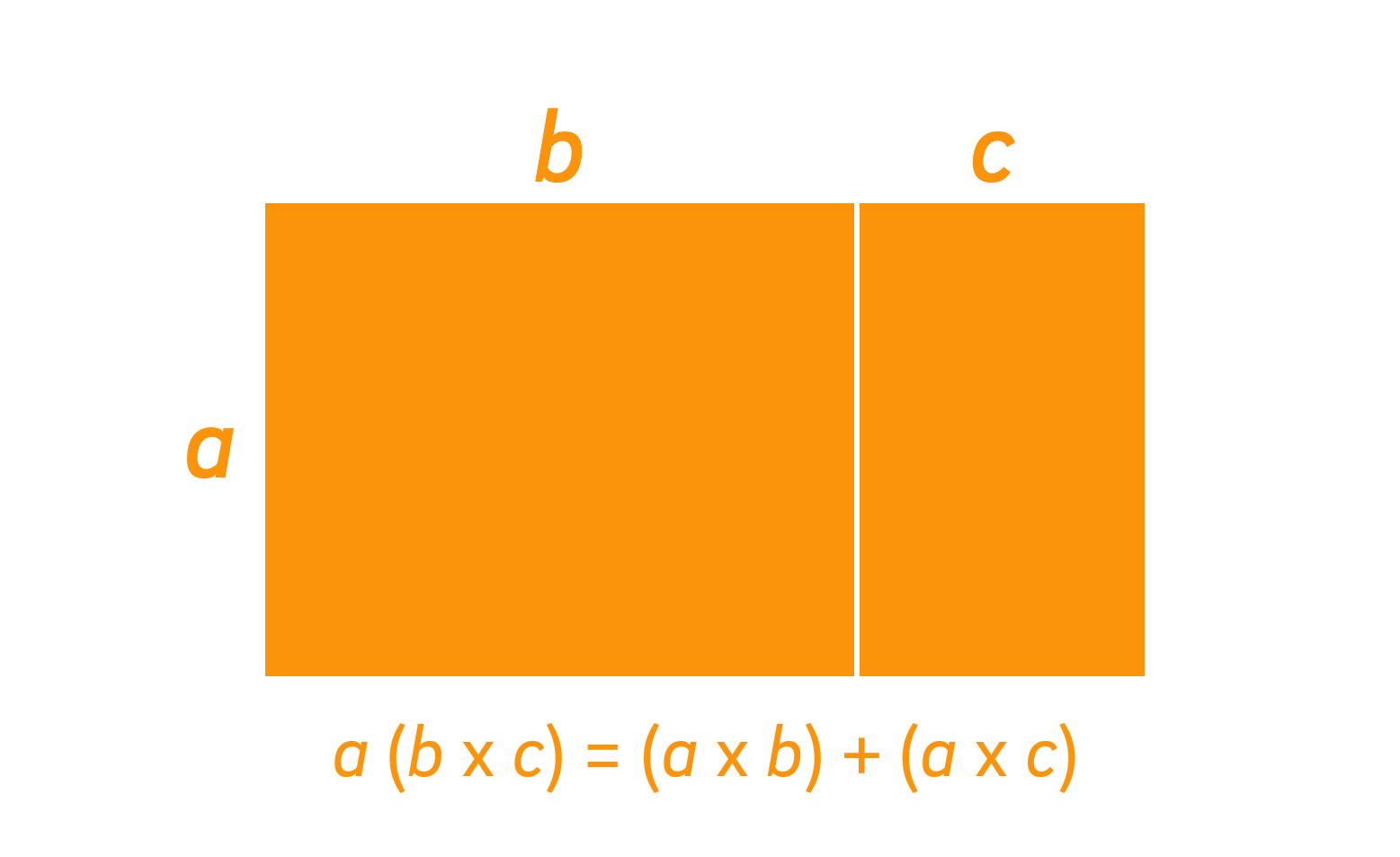
Let’s consider the distributive property applied to $12 \times 4$:
12 can be partitioned into $10 + 2$. Each part is then multiplied by 4. The partial products formed are then added together to find the total.
This can be represented using following equation:
$$12 \times 4 = (10 \times 4) + (2 \times 4)$$
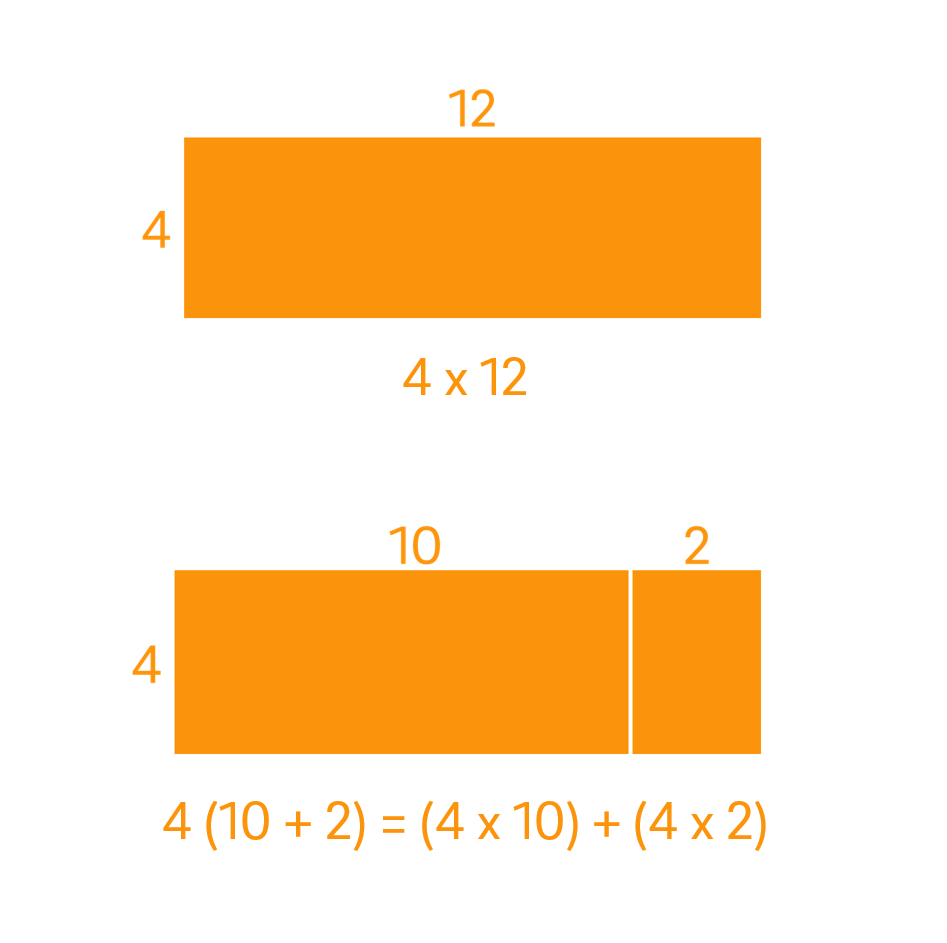
It is called the distributive property because the 4 is distributed across the 10 and the 2.
Associative property of multiplication
This task provides a context for students to continue to explore the associative property of multiplication. The associative property is a fundamental property of our number system, that applies to addition and multiplication.
The addition or multiplication of a set of numbers gives the same output no matter how the numbers are grouped. This is known as the associative property.
In multiplication, this can be expressed algebraically as:
$$(a \times b) \times c = a \times (b \times c)$$
Let’s consider the associative property applied to $5 \times 2 \times 4$:
This can be solved as $(5 \times 2) \times 4$ or $10 \times 4$. It can also be solved as $5 \times (2 \times 4)$ or $5 \times 8$. We can represent this in the following way:
$$(5 \times 2) \times 4 = 5 (2 \times 4)$$
$$10 \times 4 = 5 \times 8$$
This task provides a context for students to continue to explore the associative property of multiplication. The associative property is a fundamental property of our number system, that applies to addition and multiplication.
The addition or multiplication of a set of numbers gives the same output no matter how the numbers are grouped. This is known as the associative property.
In multiplication, this can be expressed algebraically as:
$$(a \times b) \times c = a \times (b \times c)$$
Let’s consider the associative property applied to $5 \times 2 \times 4$:
This can be solved as $(5 \times 2) \times 4$ or $10 \times 4$. It can also be solved as $5 \times (2 \times 4)$ or $5 \times 8$. We can represent this in the following way:
$$(5 \times 2) \times 4 = 5 (2 \times 4)$$
$$10 \times 4 = 5 \times 8$$
Ask students to create their own card sort activity using the following instructions. These instructions are on slide 38 of the Trays of arrays PowerPoint.
- Start by selecting a multiplication problem.
- Think of at least three different ways that the multiplication problem can be solved.
- Represent the different solution methods as an array and as an equation.
- Create a card for each array and for each equation.
Have students swap their card sort activity with another person/group and ask them to solve it.
Assessment
This activity can be used as an assessment task with students. Look at the different arrays and equations created as part of their card sort.
- Can they solve one multiplication problem using different strategies and can they accurately represent these different strategies?
- Can they accurately represent a given strategy using an array and an equation?
- Do they provide a mathematically sound justification as to which strategy is their preferred strategy for a given problem?
This activity can be used as an assessment task with students. Look at the different arrays and equations created as part of their card sort.
- Can they solve one multiplication problem using different strategies and can they accurately represent these different strategies?
- Can they accurately represent a given strategy using an array and an equation?
- Do they provide a mathematically sound justification as to which strategy is their preferred strategy for a given problem?