Multiplication: Trays of arrays
View Sequence overviewIn multiplication, factors can be partitioned and distributed to make partial products. Partitioning factors to create well-known multiplication facts, such as multiples of ten, is particularly helpful. The partial products are then added together to find the product of the original multiplication. This property is known as the distributive property of multiplication.
Whole class
Trays of arrays PowerPoint
Each group
Blank A3 paper
Bread roll array picture, printed on A4 paper and cut in half
Task
Use Trays of arrays PowerPoint to continue the story of the reSolve Bakery. Show students the illustration on slide 10.
Revise the previous task: We can calculate the total number of objects in an array by partitioning the large array into smaller arrays. The total number of objects in the smaller arrays are then added together to find the total number of objects in the large array.
Show the picture of the bread roll array on slide 11.
Each day, four different types of bread rolls are made in the reSolve Bakery.
Pose the task: How might you partition the larger array into smaller arrays to determine how many bread rolls there are altogether?
Revise
The tasks in the sequence have been ordered so that new learning in this task is built on the learning from the previous tasks. We suggest that you start each task by revising the key idea from the previous task. In this task, students are asked to apply the understanding developed in Task 1 to a new context.
The tasks in the sequence have been ordered so that new learning in this task is built on the learning from the previous tasks. We suggest that you start each task by revising the key idea from the previous task. In this task, students are asked to apply the understanding developed in Task 1 to a new context.
Provide each pair with a sheet of A3 paper to create a poster of their solutions strategies. Also provide access to Bread roll array picture to use if they choose.
Encourage students to think of different ways they might partition the large array of bread rolls into smaller arrays. Students should record the different solutions that they come up with on their poster, along with the following information:
- At least two different ways that the large array can be partitioned into smaller arrays.
- Which partitioning method is their preferred strategy for working out the total in the collection and why.
Take note of the ways that students are partitioning the larger array.
- Are the students partitioning the smaller arrays of bread rolls or are they looking at the larger array of rolls? Prompt students to think about how they might partition the large array.
- Are students identifying known multiplication facts and partitioning the array based on these facts? Prompt students to consider the multiplication facts that they know well and how they might use these facts to help them find out how many bread rolls there are altogether.
Also observe whether students apply their understanding from Task 1 to this task.
- Do students partition the full array and add together all the partial products formed to find the total?
- What multiplication facts do you know? Which ones can be found by partitioning the larger array?
- Students can use any multiplication facts based on multiples of 1, 2, 3 and 4.
- Which multiplication facts cannot be found by partitioning the larger array?
- It is not possible to create facts like 5 x 10 or 10 x 10 just by partitioning the larger array. The arrays would need to be partitioned and then rearranged.
- Which is your preferred way of partitioning the array to find the total number of bread rolls?
- Students’ answers should be focused on finding arrays of well-known facts in the larger array. Partitioning numbers based on place value is very efficient.
The distributive property
Students are asked to partition the array into smaller parts to solve this problem. They are being asked to apply the distributive property of multiplication. The distributive property is a fundamental arithmetic property of our number system.
In multiplication, numbers can be partitioned and distributed to make partial products. The partial products are then added together to find the original total of the multiplication. This is known as the distributive property of multiplication.
This can be expressed algebraically as:
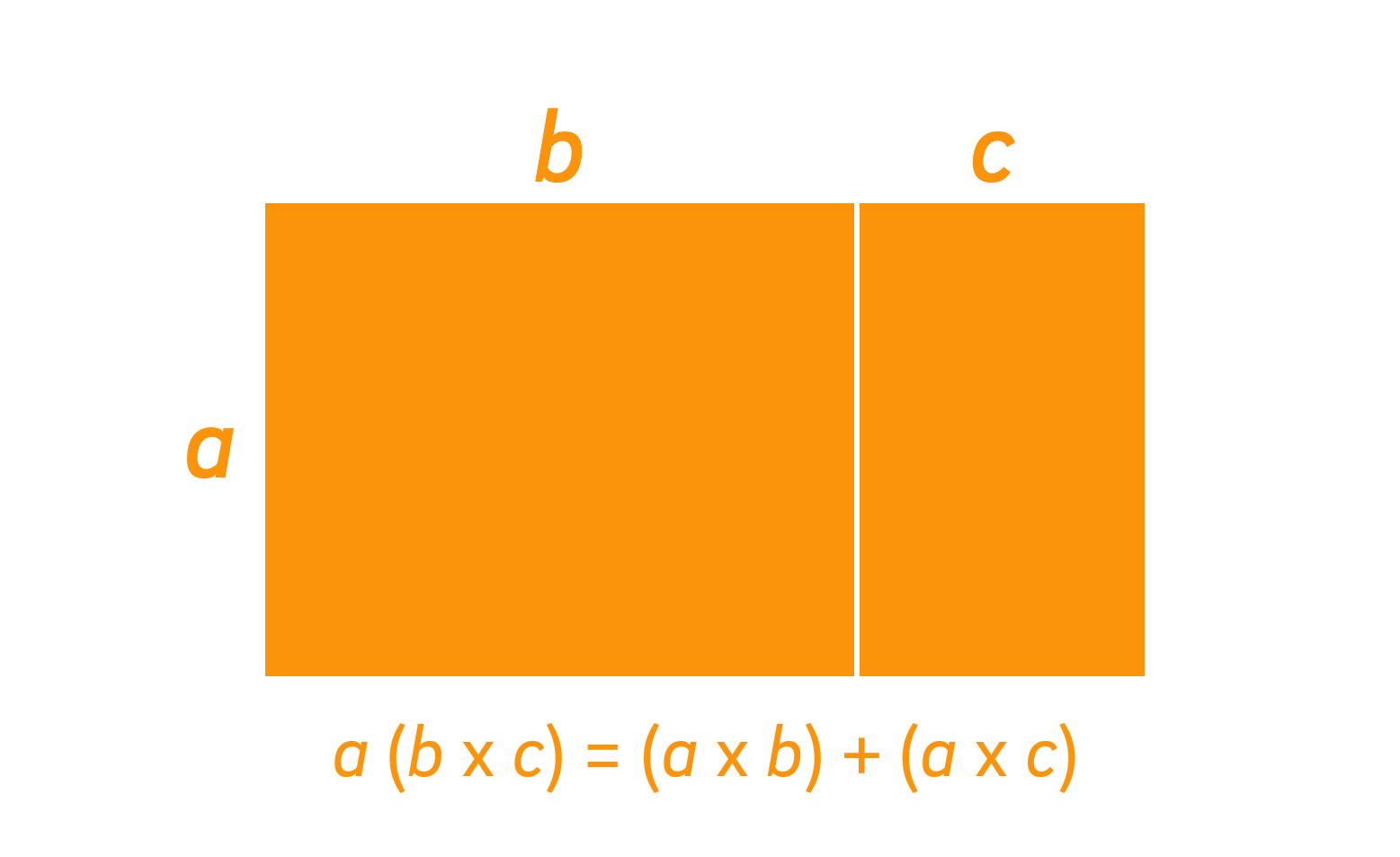
Let’s consider the distributive property applied to $12 \times 4$:
12 can be partitioned into $10 + 2$. Each part is then multiplied by 4. The partial products formed are then added together to find the total.
This can be represented using following equation:
$$12 \times 4 = (10 \times 4) + (2 \times 4)$$
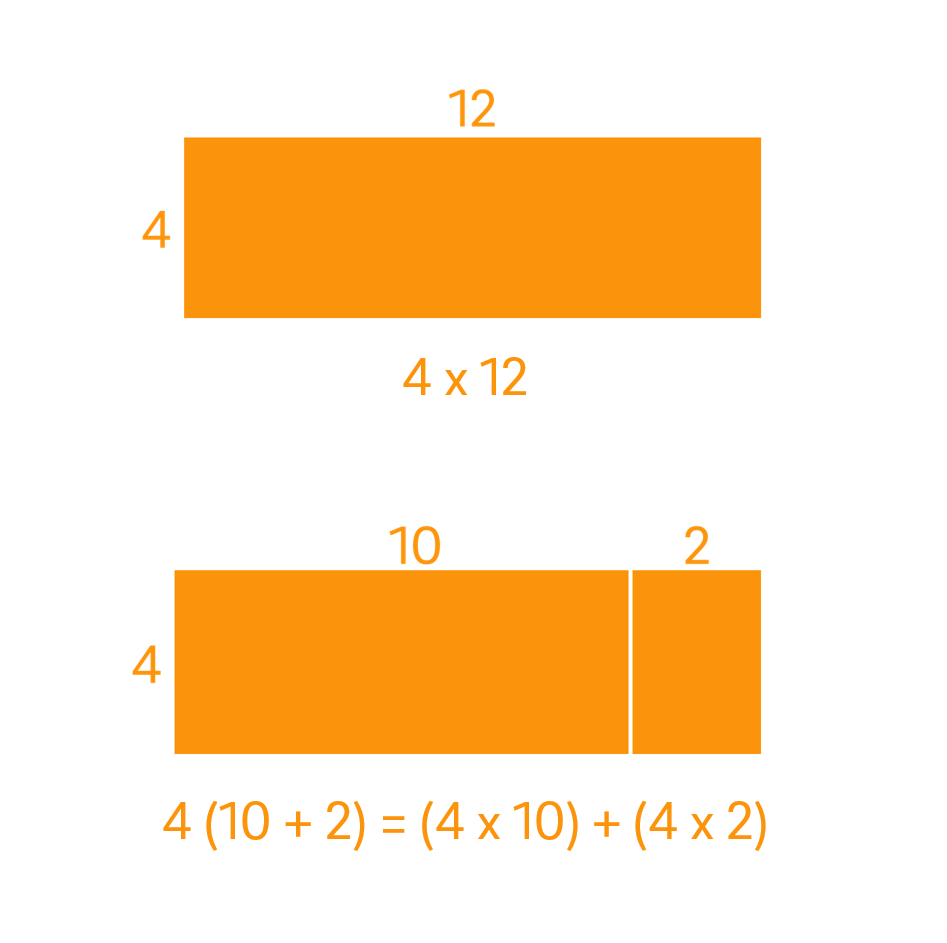
It is called the distributive property because the 4 is distributed across the 10 and the 2.
Students are asked to partition the array into smaller parts to solve this problem. They are being asked to apply the distributive property of multiplication. The distributive property is a fundamental arithmetic property of our number system.
In multiplication, numbers can be partitioned and distributed to make partial products. The partial products are then added together to find the original total of the multiplication. This is known as the distributive property of multiplication.
This can be expressed algebraically as:
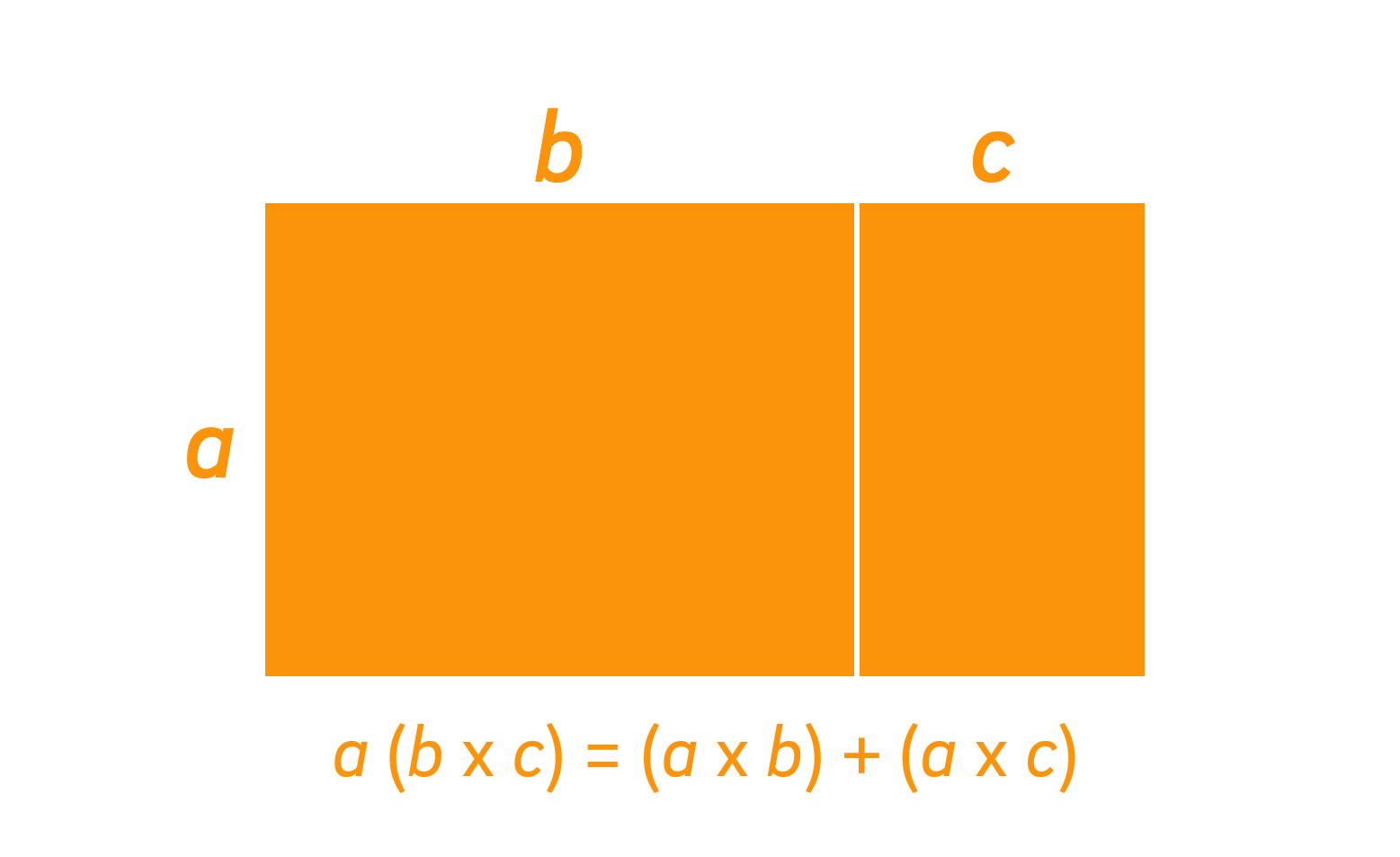
Let’s consider the distributive property applied to $12 \times 4$:
12 can be partitioned into $10 + 2$. Each part is then multiplied by 4. The partial products formed are then added together to find the total.
This can be represented using following equation:
$$12 \times 4 = (10 \times 4) + (2 \times 4)$$
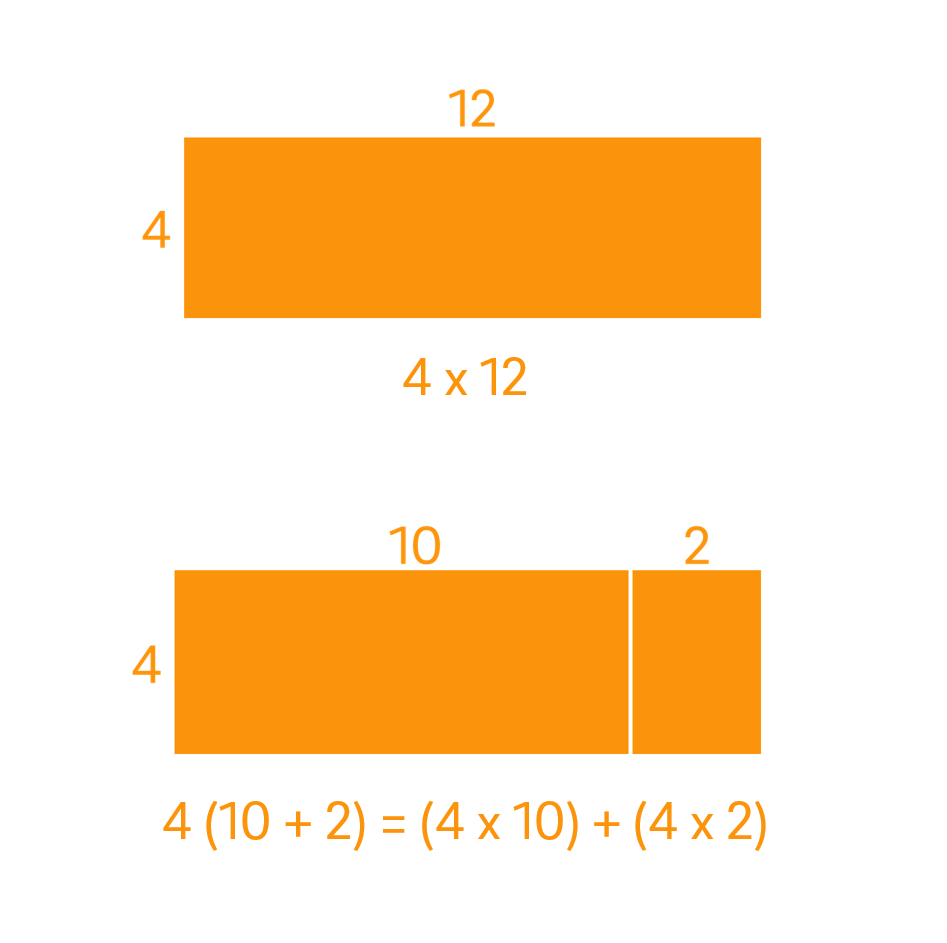
It is called the distributive property because the 4 is distributed across the 10 and the 2.
Work samples
Look at how these students have solved the problem.
Discuss with colleagues: What do these students know and what have they shown that they can do? Give evidence from the work samples for your statements.
Look at how these students have solved the problem.
Discuss with colleagues: What do these students know and what have they shown that they can do? Give evidence from the work samples for your statements.
Select some students to share the strategies they used to calculate the total number of bread rolls in the array. Model students’ strategies using an open array (area model) and record as an equation. The Model students' strategies professional learning embedded in this step illustrates how you might do this.
Discuss:
- How are the strategies used different, and how are they similar?
- Difference is seen in the way the array has been partitioned. Similarity is seen in the fact that the array is partitioned. This points to the multiplicative property of distributivity.
- Which way of partitioning the array was most helpful in calculating the total number of bread rolls?
- We need to consider the factors (that is, the numbers being multiplied) in the problem to decide which ways of partitioning are most helpful.
- Multiplication by whole tens is efficient and is also foundational to using the formal multiplication algorithm in later years. As the bread rolls are in smaller 4 x 6 arrays it is not immediately obvious that you can partition based on ten. Students should see that partitioning the array based on the place value parts of numbers is a helpful strategy.
Connect discussion
The focus of this discussion is to look at efficiency. Students will have partitioned the array in multiple different ways. It is likely that a number of these ways will not be an efficient way to calculate the total. For example, $24 \times 4$ can be solved by partitioning 24 into 10 and 14 and creating the following equation
$$24 \times 4 = (10 \times 4) + (14 \times 4)$$
This is correct use of the distributive property, however it is not a necessarily helpful use of the property, unless I know my 14-times tables off the top of my head!
Partitioning the 24 into 10, 10 and 4 is more helpful as the partial products formed are all likely to be known facts. It also forms partial products that are whole tens which makes adding the products together easier.
$$24 \times 4 = (10 \times 4) + (10 \times 4) + (4 \times 4)$$
If students can multiply by whole tens, then partitioning 24 into 20 and 4 is more efficient again.
$$24 \times 4 = (20 \times 4) + (4 \times 4)$$
Partitioning based on place value is typically the most efficient way to solve multi-digit multiplication problems. Place valuing partitioning is also the basis for the formal multiplication algorithm which students will learn in later years.
The focus of this discussion is to look at efficiency. Students will have partitioned the array in multiple different ways. It is likely that a number of these ways will not be an efficient way to calculate the total. For example, $24 \times 4$ can be solved by partitioning 24 into 10 and 14 and creating the following equation
$$24 \times 4 = (10 \times 4) + (14 \times 4)$$
This is correct use of the distributive property, however it is not a necessarily helpful use of the property, unless I know my 14-times tables off the top of my head!
Partitioning the 24 into 10, 10 and 4 is more helpful as the partial products formed are all likely to be known facts. It also forms partial products that are whole tens which makes adding the products together easier.
$$24 \times 4 = (10 \times 4) + (10 \times 4) + (4 \times 4)$$
If students can multiply by whole tens, then partitioning 24 into 20 and 4 is more efficient again.
$$24 \times 4 = (20 \times 4) + (4 \times 4)$$
Partitioning based on place value is typically the most efficient way to solve multi-digit multiplication problems. Place valuing partitioning is also the basis for the formal multiplication algorithm which students will learn in later years.
Model students’ strategies
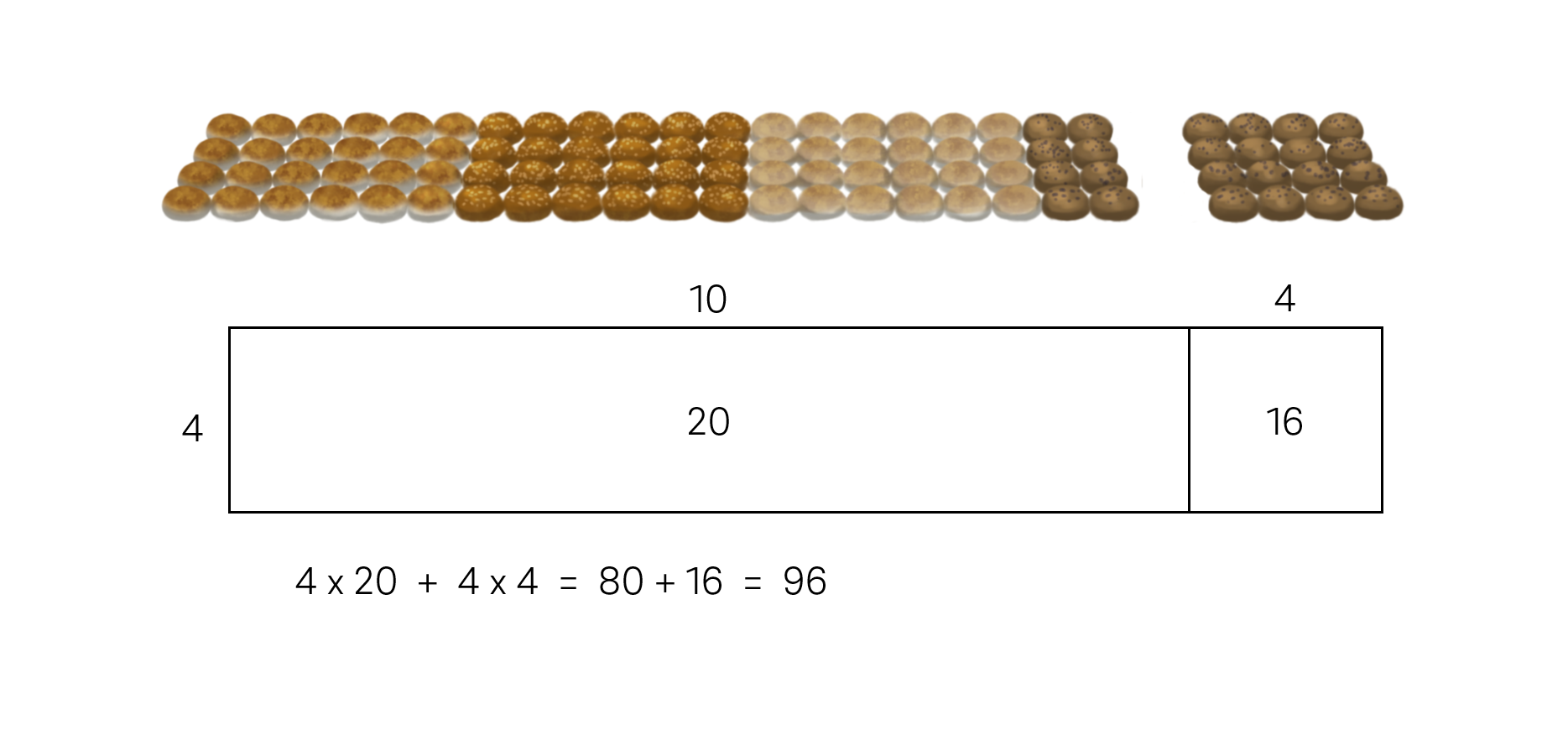
We want students to represent their thinking using multiple representations, and to see how these different representations are connected. Below are three examples of students’ strategies and how you might model students’ strategies using an open array (area model) and with an equation. These three strategies are different, yet similarities can be seen in the equations.
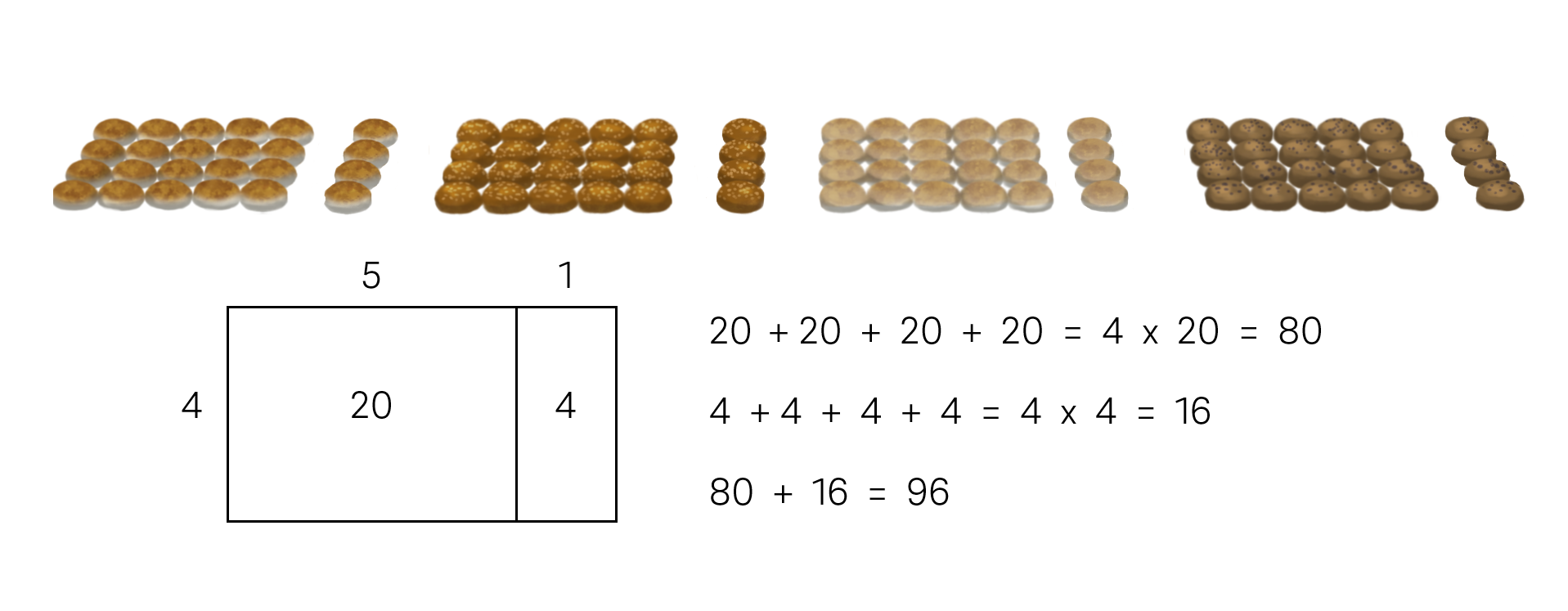
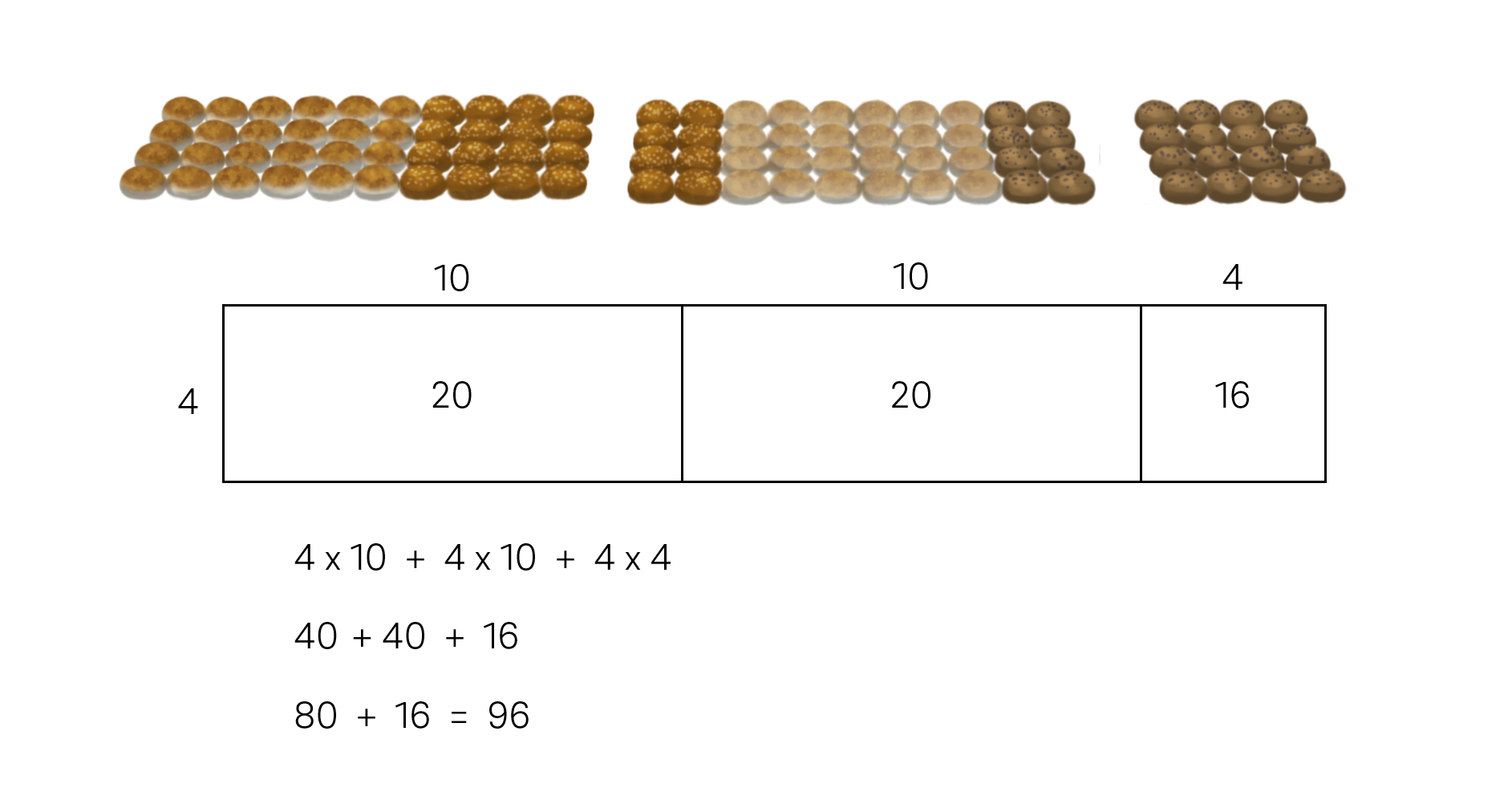
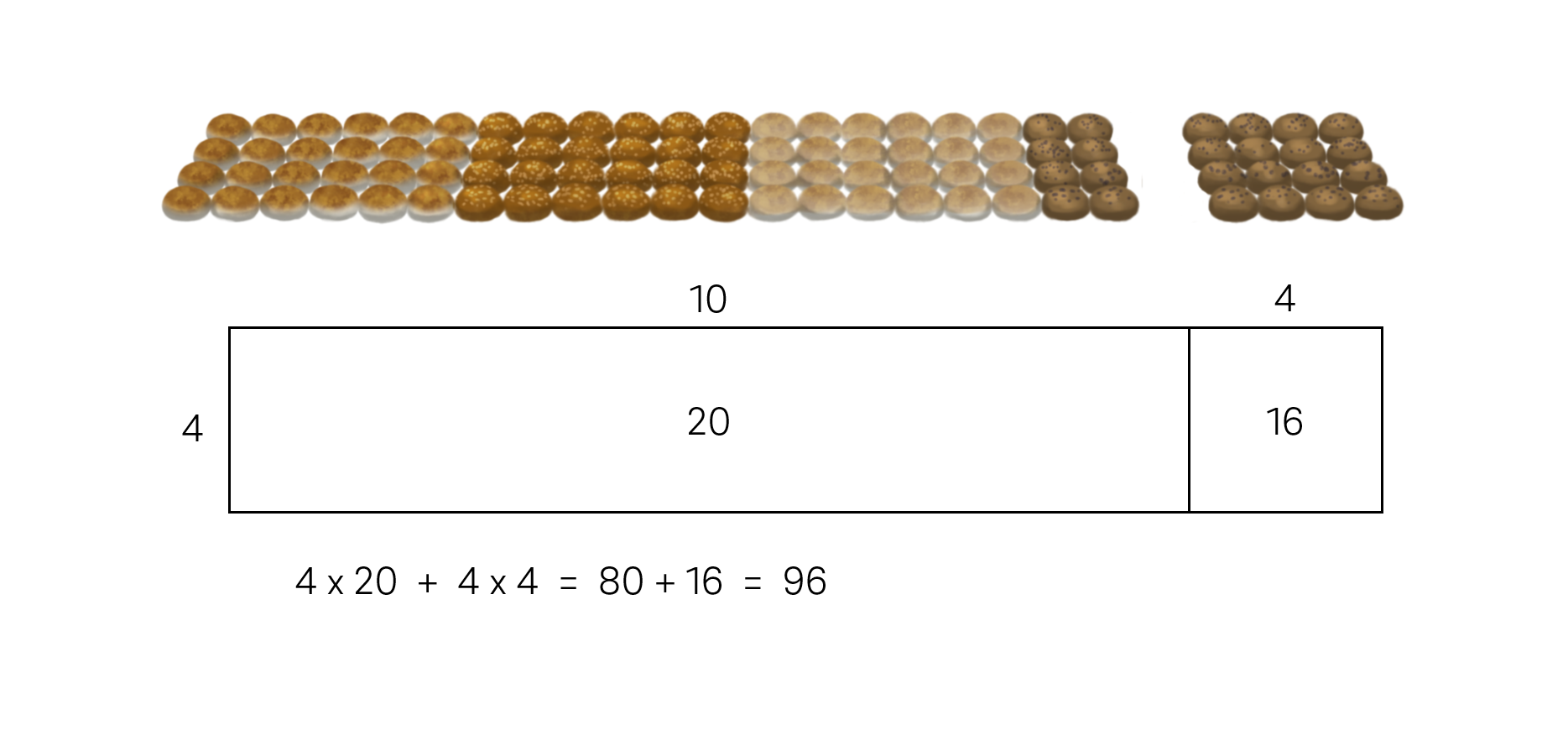
We want students to represent their thinking using multiple representations, and to see how these different representations are connected. Below are three examples of students’ strategies and how you might model students’ strategies using an open array (area model) and with an equation. These three strategies are different, yet similarities can be seen in the equations.
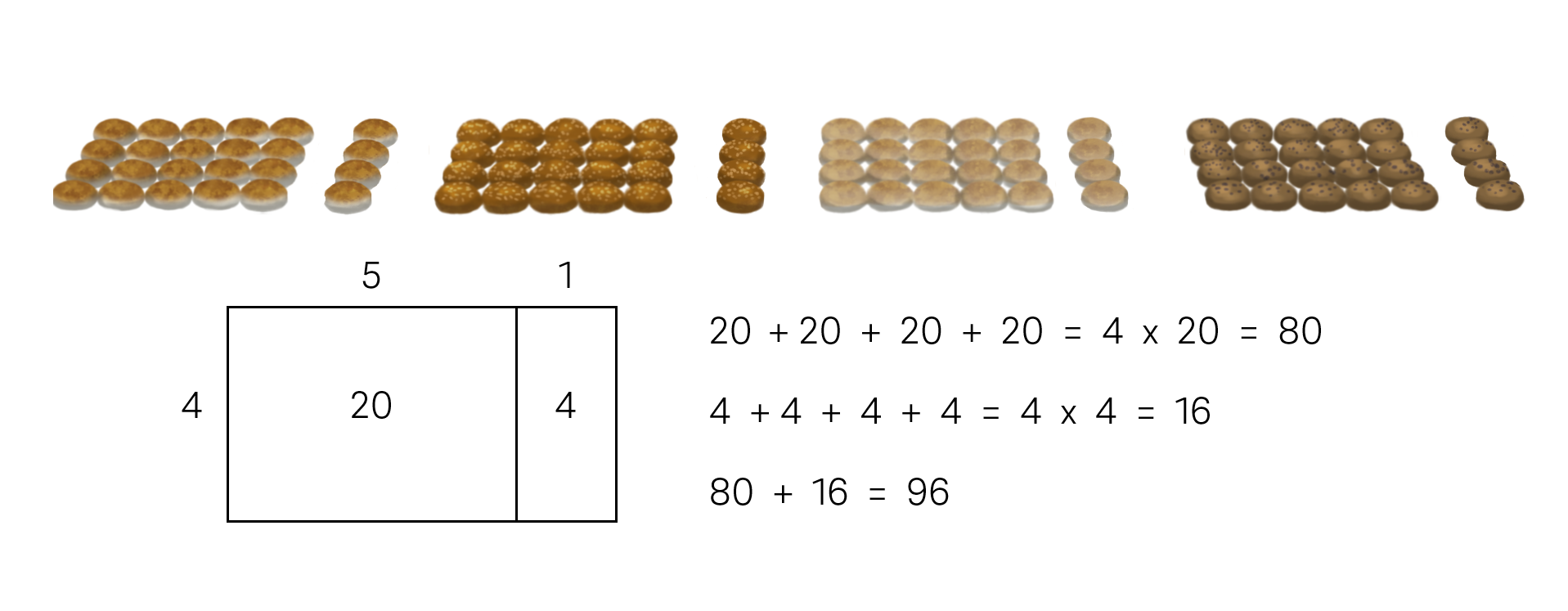
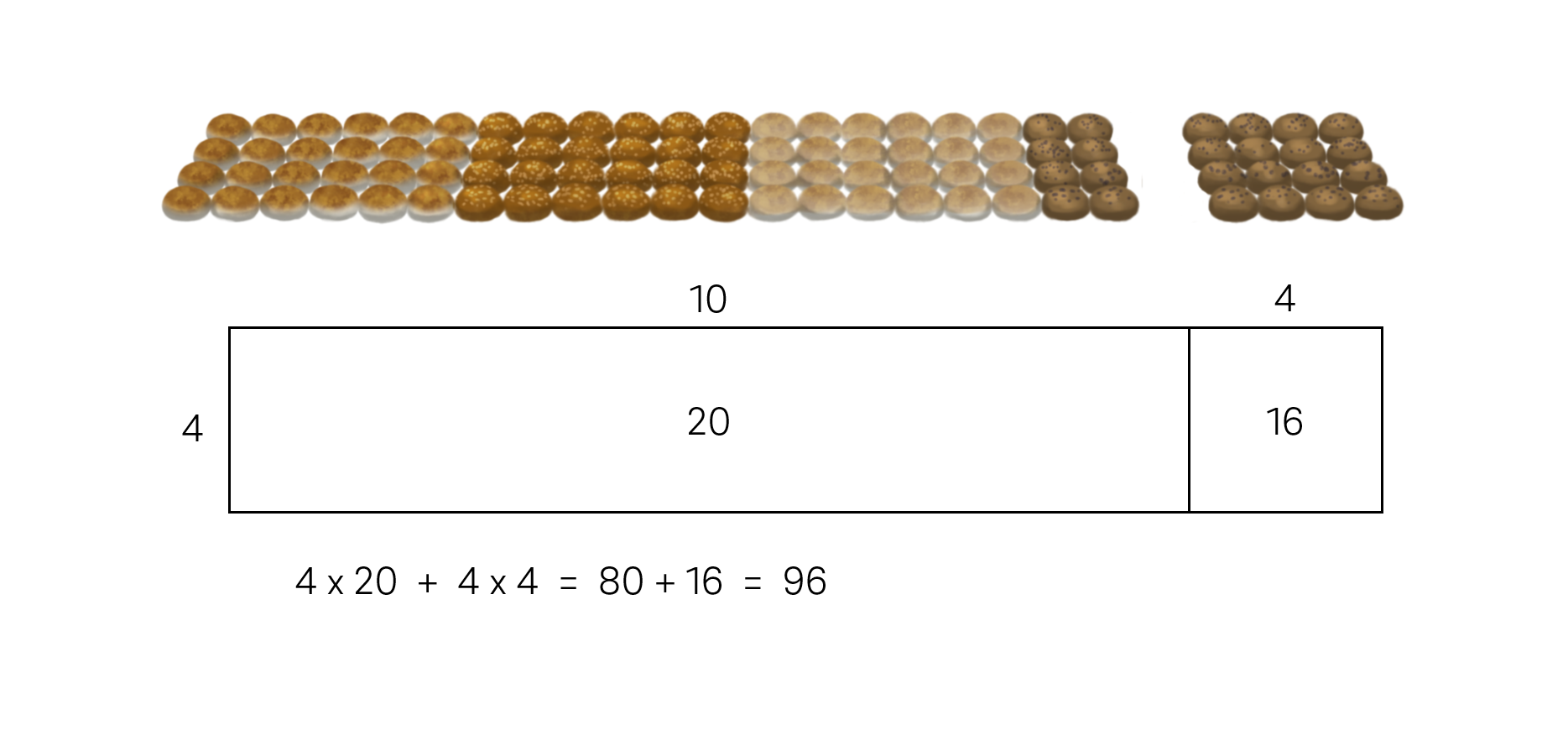
Explain: We can solve a difficult multiplication problem by partitioning factors to create smaller problems. Partitioning factors to create well-known multiplication facts, such as multiples of ten, is particularly helpful. The products of these smaller problems are then added together to find the product of the original problem.
Discuss with students the different ways that they partitioned the factors to create known multiplication facts, such as multiples of ten, to solve the problem.
Add to the class display using the students' posters from this task, using the summary statement from above as a title for the display. Read the Class display professional learning embedded in this step to learn how this display can be used to build a shared understanding amongst the students.
Shared understanding
In the Summarise phase, the following statement is presented to students:
We can solve a difficult multiplication by partitioning factors to create smaller problems. Partitioning factors to create well-known facts, such as tens, is particularly helpful. The products of these smaller problems are then added together to find the product of the original problem.
This statement reflects the learning goal for the task and is the understanding that we want all in the class to share. As the sequence progresses, this shared understanding is built on.
As with the last task, we suggest you create a new display of students’ work with this statement. Present this display next to the display of work from the last task. This provides the opportunity for students to revisit and reflect on this understanding and the ways that that it is reflected in the different solutions strategies used by students. The display is a way to help ensure the understanding is truly shared by all in the class. Students can also see how their shared understanding is developing through the sequence.
Presenting everyone’s work with this statement communicates that everyone has contributed to and participated in developing this understanding as shared in the class, regardless of how complex or sophisticated their thinking may or may not be.
In the Summarise phase, the following statement is presented to students:
We can solve a difficult multiplication by partitioning factors to create smaller problems. Partitioning factors to create well-known facts, such as tens, is particularly helpful. The products of these smaller problems are then added together to find the product of the original problem.
This statement reflects the learning goal for the task and is the understanding that we want all in the class to share. As the sequence progresses, this shared understanding is built on.
As with the last task, we suggest you create a new display of students’ work with this statement. Present this display next to the display of work from the last task. This provides the opportunity for students to revisit and reflect on this understanding and the ways that that it is reflected in the different solutions strategies used by students. The display is a way to help ensure the understanding is truly shared by all in the class. Students can also see how their shared understanding is developing through the sequence.
Presenting everyone’s work with this statement communicates that everyone has contributed to and participated in developing this understanding as shared in the class, regardless of how complex or sophisticated their thinking may or may not be.