Multiplication: Trays of arrays
View Sequence overviewIn multiplication, numbers can be partitioned and distributed to make partial products. Partitioning numbers to create known multiplication facts, such as multiples of ten, is particularly helpful. The partial products are then added together to find the original total of the multiplication. This is the distributive property of multiplication.
Whole class
Trays of arrays PowerPoint
Each group
Small collections of counters
Each student
How can I work it out? Student sheet
At least 1 sheet of grid paper
Post-it notes for use in the gallery walk
Build
Complete the number strings below as a class. We suggest completing the string on two separate days (see the Suggested Implementation for this sequence).
The first number string is on slide 13 and the second is on slide 14.
| Number string 1 | Number string 2 |
$$2 \times 6$$ $$5 \times 6$$ $$7 \times 6$$ $$10 \times 6$$ $$17 \times 6$$ $$27 \times 6$$ $$6 \times 52$$ | $$9 \times 10$$ $$9 \times 9$$ $$9 \times 11$$ $$9 \times 3$$ $$9 \times 13$$ $$9 \times 15$$ |
Distributive property

These number strings have been carefully crafted to build students’ understanding of the distributive property.
Let’s look closely at the first string.
The first two problems, $2 \times 6$ and $5 \times 6$, are likely to be known multiplication facts for most students. The answers to these two facts can be used to calculate the total of $7 \times 6$.
The fourth question, $10 \times 6$, is also likely to be a known fact for most students. Every subsequent problem can be solved by using the answers to previous questions. For example, $15 \times 6$ can be solved by adding together the answer to $10 \times 6$ and the answer to $5 \times 6$.
Use an array and equations to represent students’ strategies. The Number strings professional learning video embedded in this step illustrates how you might do this.
Discuss with colleagues: What relationships do you notice between the numbers in the second string?
These number strings have been carefully crafted to build students’ understanding of the distributive property.
Let’s look closely at the first string.
The first two problems, $2 \times 6$ and $5 \times 6$, are likely to be known multiplication facts for most students. The answers to these two facts can be used to calculate the total of $7 \times 6$.
The fourth question, $10 \times 6$, is also likely to be a known fact for most students. Every subsequent problem can be solved by using the answers to previous questions. For example, $15 \times 6$ can be solved by adding together the answer to $10 \times 6$ and the answer to $5 \times 6$.
Use an array and equations to represent students’ strategies. The Number strings professional learning video embedded in this step illustrates how you might do this.
Discuss with colleagues: What relationships do you notice between the numbers in the second string?
Revise: We have learnt that we can solve a difficult multiplication problem by partitioning factors to create smaller problems. Partitioning factors to create well-known multiplication facts, such as multiples of ten, is particularly helpful. The products of these smaller problems are then added together to find the product of the original problem.
Show students slide 15 in the Trays of arrays PowerPoint.
Pose the activity: These students know how to multiply by 2, 3, 5, and 10. Can you show them how they can use what they do know to work out what they don’t know?
Provide students with How can I work it out? Student sheet. Allow them time to work through the activity.
Ask students to present their different solutions as array. They may choose to use grid paper or counters to do this.
Solving multiplication problems

Students are asked to partition the array into smaller parts to solve these different multiplication problems. They are being asked to apply the distributive property of multiplication. The distributive property is a fundamental arithmetic property of our number system.
In multiplication, numbers can be partitioned and distributed to make partial products. The partial products are then added together to find the original total of the multiplication. This is known as the distributive property of multiplication.
This can be expressed algebraically as:
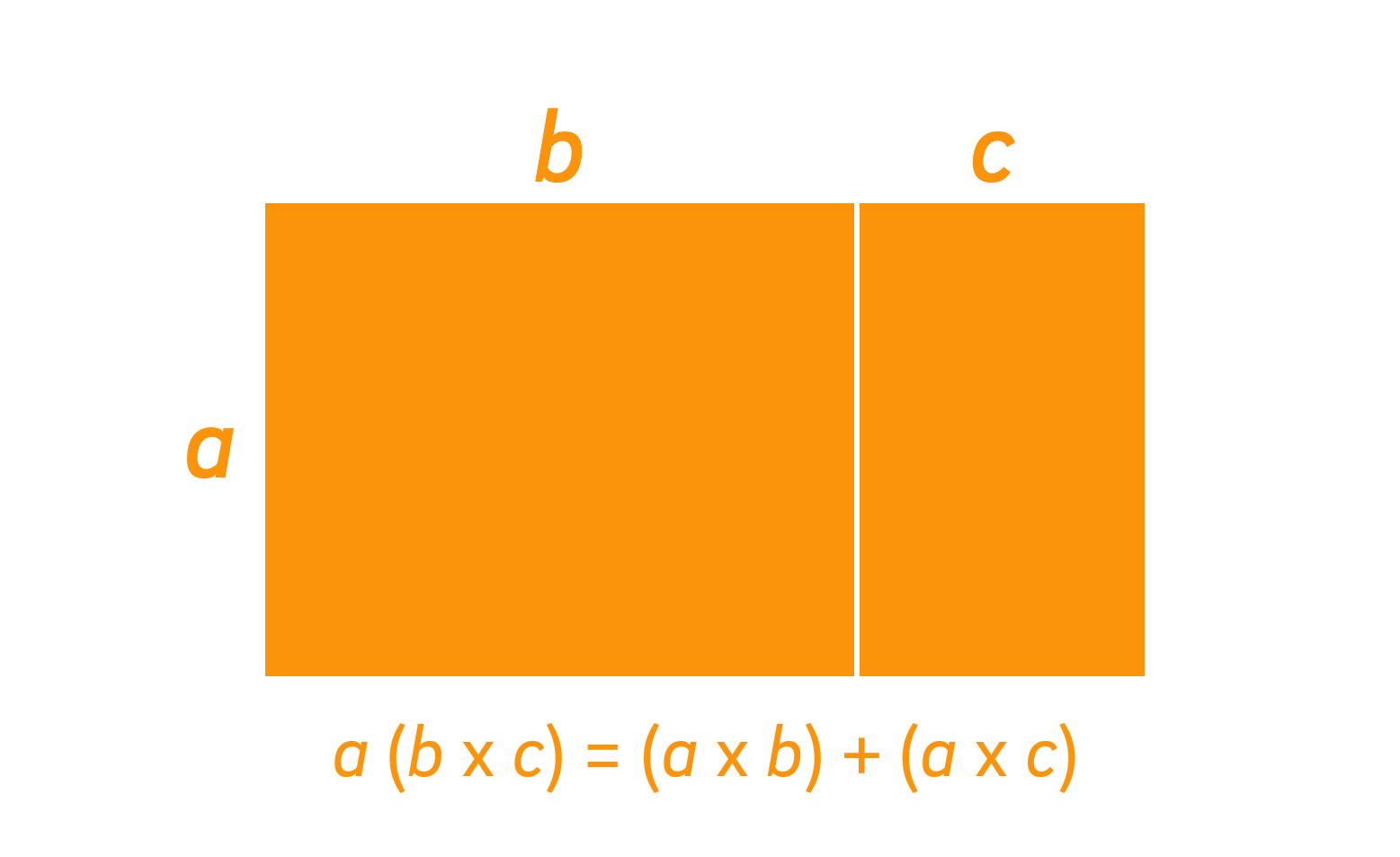
Let’s consider the distributive property applied to $12 \times 4$:
12 can be partitioned into $10 + 2$. Each part is then multiplied by 4. The partial products formed are then added together to find the total.
This can be represented using following equation:
$$12 \times 4 = (10 \times 4) + (2 \times 4)$$
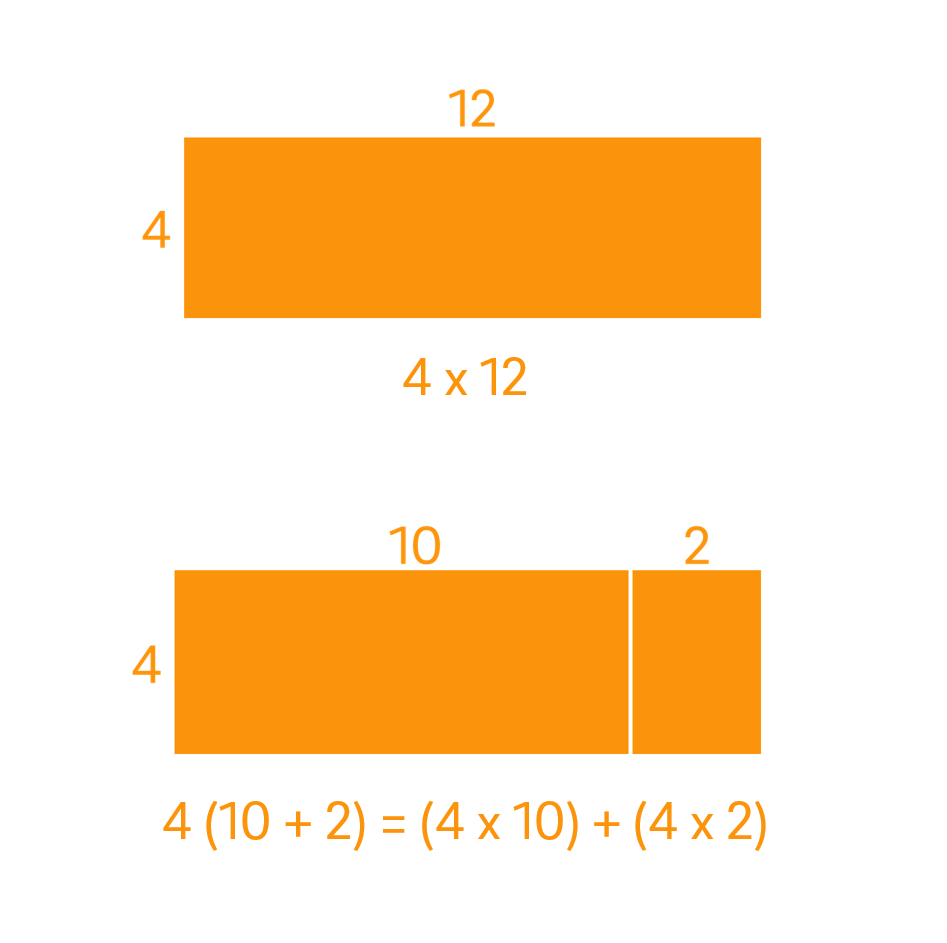
It is called the distributive property because the 4 is distributed across the 10 and the 2.
Students are asked to partition the array into smaller parts to solve these different multiplication problems. They are being asked to apply the distributive property of multiplication. The distributive property is a fundamental arithmetic property of our number system.
In multiplication, numbers can be partitioned and distributed to make partial products. The partial products are then added together to find the original total of the multiplication. This is known as the distributive property of multiplication.
This can be expressed algebraically as:
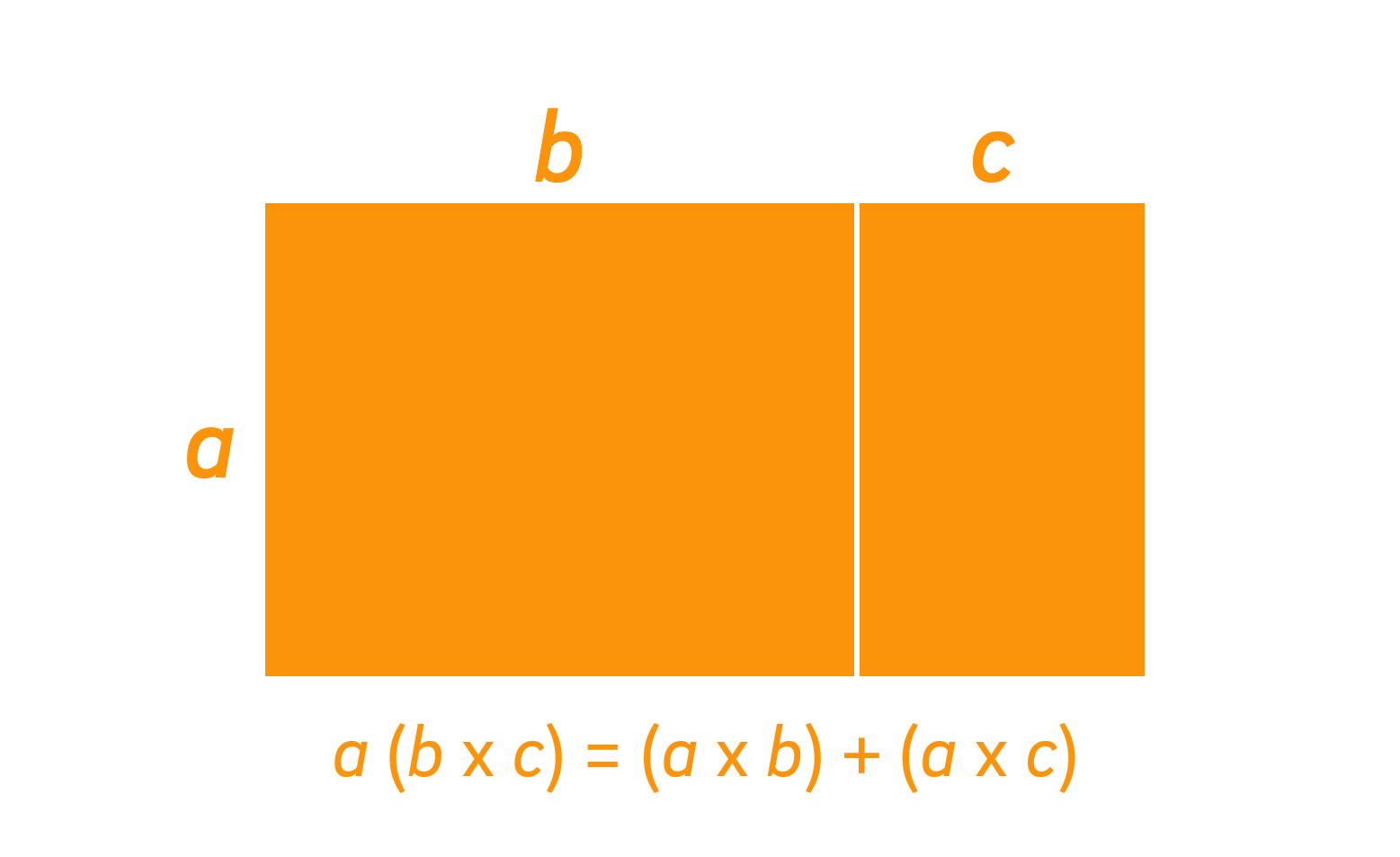
Let’s consider the distributive property applied to $12 \times 4$:
12 can be partitioned into $10 + 2$. Each part is then multiplied by 4. The partial products formed are then added together to find the total.
This can be represented using following equation:
$$12 \times 4 = (10 \times 4) + (2 \times 4)$$
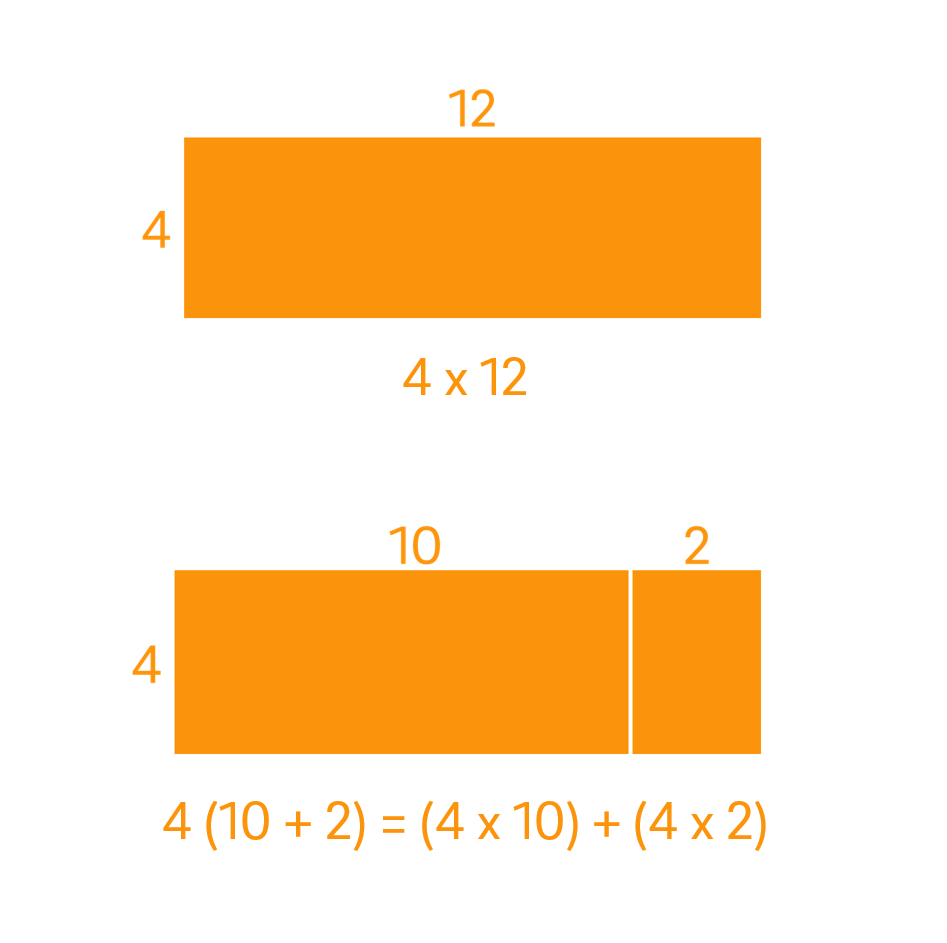
It is called the distributive property because the 4 is distributed across the 10 and the 2.
Conduct a gallery walk so that students can look at the different solutions that other students have used. Ask students to consider the following questions in the gallery walk:
- Look at how other students have solved the problems. What do you notice?
- Are there strategies that are different to the strategy that you used? Which strategies were particularly helpful for working out the different problems? Why?
Conduct a class discussion to look at the different solutions that the students used to solve the different multiplication problems.