Mathematical modelling: Playing with fire
View Sequence overviewA rule of thumb is a quick and simple way to make an estimate; however, a mathematical model provides greater precision.
Whole class
Playing with fire PowerPoint
Playing with fire Spreadsheet (Teacher)
Each group
Playing with fire Spreadsheet (Student)
Access to computer, at least 1 between 3 students
Lesson
Show students slide 21 of Playing with Fire PowerPoint to review the previous lesson. Discuss how wind speed influences the rate of fire spread and explain how we can estimate the forward rate of spread using a rule of thumb based on this relationship.
Provide students with computer access and the Playing with fire Spreadsheet (Student). Ask students to open the second sheet titled Wind estimates, which contains the same table they used in the previous lesson. Ask students to, in the relevant column, create a formula based on the rule of thumb that the forward rate of fire spread is 10% of the wind speed measured at 10 m above ground level.
The sheet titled Wind estimates in the Playing with fire Spreadsheet (Teacher) is completed for reference.
To calculate the rate of spread based on the rule of thumb, we can use the following formula:
$$\text{wind speed} \times 0.1 \times 1000$$
This formula multiplies the wind speed by 0.1 to apply the rule of thumb, and then multiplies the result by 1000 to convert from kilometres per hour to metres per hour.
To use this formula in the spreadsheet, enter the following formula into cell L4, the first cell in the Rule of thumb column. The table is set up so that entering the formula in the top cell will automatically populate the rest of the column.
=0.1 * E4 * 1000
Where E4 = 10m wind speed (km/h)
This provides a good opportunity for discussion with students about simplifying formulas. Since $0.1\times1000$ is equal to 100, the formula can be simplified to:
=100 * E4
Both versions produce the same result. Exploring this equivalence can help reinforce students’ understanding the commutative property of multiplication.
Using digital tools
Digital tools allow calculations to be processed quickly. In this lesson, students use a spreadsheet and write simple code to calculate the forward rate of spread of a fire. The focus is not on performing the calculations manually, but on evaluating the accuracy of a rule of thumb compared to a formal mathematical model. For this reason, we recommend using spreadsheet software. Automating the process allows students to focus on analysing the accuracy and reliability of each approach, which occurs later in this lesson.
Digital tools allow calculations to be processed quickly. In this lesson, students use a spreadsheet and write simple code to calculate the forward rate of spread of a fire. The focus is not on performing the calculations manually, but on evaluating the accuracy of a rule of thumb compared to a formal mathematical model. For this reason, we recommend using spreadsheet software. Automating the process allows students to focus on analysing the accuracy and reliability of each approach, which occurs later in this lesson.
Ask: Compare the predicted rate of spread to the observed forward rate of spread. How accurate are our predictions when using the rule of thumb? Students can compare values visually, or they can add an extra column to their sheet and use a formula to calculate the difference between the observed and predicted rates of spread.
Invite students to share their observations and prompt them to use data to justify their claims.
Ask students to use the other data in the table to explain why some fires may be considered outliers. Encourage them to identify which fires are outliers and factors that could account for unusually fast rates of spread. For example:
- fires that spread more rapidly often occurred under conditions of higher temperatures, lower humidity, low fuel moisture content, and high fuel age.
- the rule of thumb only accounts for the influence of wind. Topography and fuel have not been considered.
Explain to students that more complex mathematical equations have been developed to estimate the rate of fire spread. These equations take environmental variables such as temperature, wind speed, relative humidity, and fuel conditions, and convert them into an estimated rate of spread.
Show slide 22 of Playing with Fire PowerPoint, which contains the following formula:
$$\text{Rate of spread} = \frac{2.518\times\text{wind speed}}{60-\text{temperature}+\text{humidity}}$$
Explain that this equation models how environmental conditions influence the forward rate of fire spread, offering a more precise alternative to the rule of thumb. It is typically used by fire managers to calculate the rate of spread for bushfires. Discuss how the equation is similar to and different from the rule of thumb.
Ask students to write a formula based on this equation in the appropriate spreadsheet column to calculate the rate of fire spread. Then, have them compare the results produced by their formula with those obtained using the rule of thumb and the actual observed rates of spread.
This formula was shared with us by Professor Jason Sharples (University of New South Wales, Canberra) and is also included in the Mathematics of Bushfires Year 9 classroom resources authored by Professor Sharples and published by the University of Melbourne. These resources complement and can be used alongside this learning sequence.
The sheet titled Wind estimates in the Playing with fire Spreadsheet (Teacher) is completed for reference.
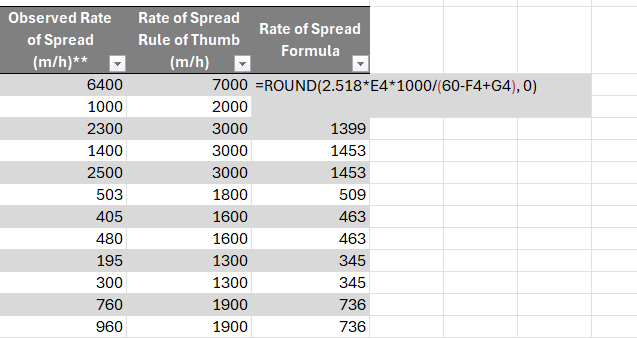
To calculate the rate of spread using the mathematical model, enter the following formula into cell M4, the first cell in the Rate of spread based on formula (m/h) column:
=ROUND(2.518 * (E4 * 1000) / (60 - F4 + G4), 0)
Where:
- E4 = Wind speed at 10 m (km/h)
- F4 = Temperature (°C)
- G4 = Relative humidity (%)
This formula:
- multiplies the wind speed by 1000 to convert from kilometres per hour to metres per hour.
- applies the given equation.
- rounds the result to the nearest whole number using ROUND(…, 0).
The table is set up so that entering the formula in the top cell automatically fills the entire column.
Discuss:
- What do you notice about the estimates using the equation and those using the rule of thumb? How do these results compare to the actual observed rate of spread?
- The estimates using the formula are typically closer to the observed rate of spread.
- What might account for some of the difference between the predicted and actual values?
- The calculations take into consideration weather factors and fuel (dry eucalypt forest). The calculations do not take into consideration topography, which is the third aspect of the fire behaviour triangle (shown on slide 23 of Playing with Fire PowerPoint as a reminder).
- If we have a proper formula that's close to the observed rate of spread, what's the point of having a rule of thumb?
- The rule of thumb is simple and quick to use in emergency situations where there is no time or technology available to apply the full mathematical model. It provides a rough estimate that can guide initial decisions before more precise data or calculations are available.
- When might the rule of thumb be 'close enough'?
The rule of thumb may be adequate when conditions are relatively stable (e.g., flat terrain, typical dry fuel conditions) and decisions need to be made rapidly. It can also be useful when high precision is not critical, such as in training scenarios or when confirming trends predicted by other models.